de ABC formule (2 afleidingen + toepassing)

De ABC- formule geeft de nulpunten van een willekeurige kwadratische vergelijking (grafiek: parabool)
    y = ax2 + bx + c
In dit artikel worden twee afleidingen van de ABC-formule gegeven.

Inleiding
Een eenvoudiger vorm van een kwadratische vergelijking ontstaat voor b = 0:
    y = ax2 + c
De nulpunten ( y = 0)

    ax2 + c = 0


Voorbeeld
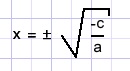
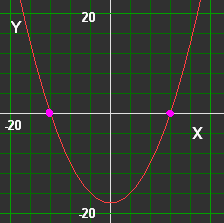We bepalen de nulpunten van y = 0,125x2 - 18
    0125x2 - 18 = 0
    x2 = 144
    x = 12 .............of...
    x = -12

Voor het geval c = 0 is het ook niet moeilijk de nulpunten te vinden.
De vergelijking gaat dan over in
    y = ax2 + bx ..................zodat
    ax2 + bx = 0
    x(ax + b) = 0
    of
    x = 0
    of
    ax + b = 0



Voorbeeld
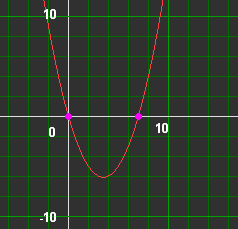We bepalen de nulpunten van y = x2 - 7x
    x2 - 7x = 0
    x(x - 7) = 0
    x = 0 .............of...
    x - 7 = 0
    x = 7


Afleiding 1...(kwadraat afsplitsen)
Bekijk de vergelijking
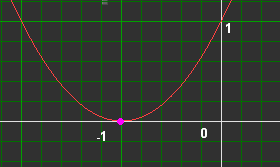
    y = x2 + 2x + 1
Deze is te herschrijven tot
    y = (x+1)2
Het nulpunt is eenvoudig te bepalen
    (x+1)2 = 0
    x + 1 = 0
    x = -1
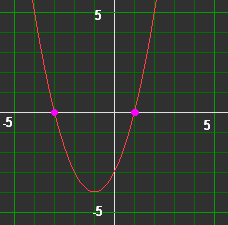
Er is maar 1 snijpunt, de parabool raakt de x-as.

Neem nu
    y = x2 + 2x - 3
Hier is geen sprake van een kwadraat zoals hiervoor,
maar dat kwadraat kunnen we wel "inbakken"
    y = x2 + 2x + 1 - 1- 3.....zodat
    y = (x+1)2 - 4
Eenmaal in deze vorm zijn de nulpunten als volgt te bepalen:
    (x+1)2 - 4 = 0
    (x+1)2 = 4
    of
    x+1 = 2
    x = 1
    of
    x+1 = -2
    x = -3
Deze methode heet "kwadraat afsplitsen".

Het komt erop neer, dat we de kwadratische vergelijking schrijven in de vorm
    y = (x + p)2 + q
    of
    y = x2 + 2px + p2 + q
De term p2 moet worden toegevoegd om het kwadraat te verkrijgen, maar
p2 moet direct weer worden afgetrokken om de vergelijking niet te veranderen.

Voorbeeld
Bekijk
    x2 - 7x + 2 = 0
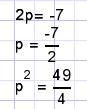
De factor -7 voor de x staat voor 2p, zodat



De vergelijking schrijven we nu in de vorm



vereenvoudigd en opgelost



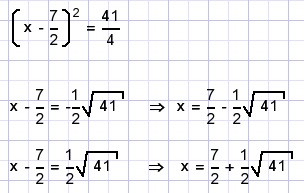
Nu dan de algemene oplossing van ax2 + bc + c = 0

Delen door a levert:



daarbij is



Zodat de vergelijking met afgesplitst kwadraat geschreven moet worden als



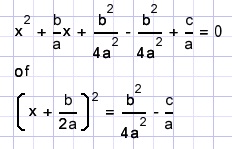
wat netter geschreven



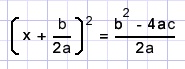
De oplossingen zijn



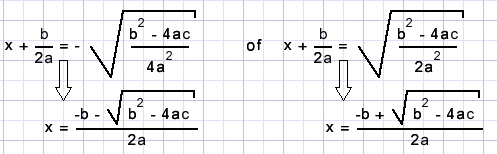
Opmerkingen
    - de nulpunten liggen symmetrisch t.o.v. de as

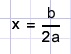
    - D = b2 - 4ac heet de "discriminant
    - voor D < 0 zijn er geen nulpunten
    - voor D = 0 is er 1 nulpunt, de parabool raakt de x-as
    - voor D > 0 zijn er 2 nulpunten
Afleiding 2...(translatie)
Als in een vergelijking x consequent wordt vervangen door (x+1) dan zal de grafiek 1 naar links schuiven.

Neem een algemene vergelijking
    ......x......y...... = .....x.....y.......
waarbij de puntjes ............ staan voor getallen en bewerkingen.
Stel eens, dat de vergelijking klopt voor x = 3 en y = 10, dus het punt (3,10) ligt op de grafiek.

Nu vervangen we (x) door (x+1), zodat
    ........(x+1)....y...........= .......(x+1).........y...........
Nu zal de vergelijking kloppen voor (x+1) = 3 en y = 10, oftewel voor het punt (2,10).
De grafiek is 1 plaats naar links geschoven.

Algemeen
    Als in een vergelijking (x) wordt vervangen door (x+h)
    dan
    zal de grafiek een afstand h naar links schuiven
nu beschouwen we de algemene vergelijking
    y = ax2 + bx + c
weglaten van c levert alleen vertikale verschuiving op.
De nulpunten zijn dan, zoals hiervoor beschreven, eenvoudig te vinden
    ax2 + bx = 0
    x(ax + b) = 0
    x = 0
    of
    ax + b = 0



Het punt tussen de 2 nulpunten is


en we verschuiven de grafiek over deze afstand, zodat dit middelpunt op de oorsprong terechtkomt.
Er geldt dus



De oorspronkelijke vergelijking gaat dan over in



Merk op:
deze formule is van het type y = Ax2 + B, de y-as is de symmetrie-as


Van de horizontaal verschoven grafiek zijn de nulpunten
    4a2x2 - b2 + 4ac = 0
    4a2x2 = b2 - 4ac


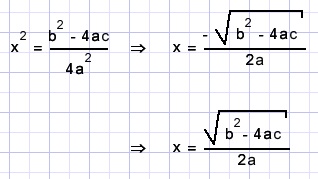
Resteert, de gevonden nulpunten weer terug te schuiven,
dat doen we door x te vervangen door

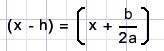
zodat



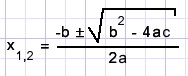
Wat in overeenstemming is met de uitkomst van methode-1

Een grappige toepassing
Een puzzle bestaat uit een bord met vakjes. In sommige vakjes staan kruisjes afgebeeld.
Die kruisjes worden opgesteld onder een horizontale lijn. Een kruisje mag horizontaal
of vertikaal over een aangrenzend kruisje in een open vakje springen.
Het kruisje waar overheen wordt gesprongen moet daarbij worden verwijderd.
Een soort "slaan" als bij dammen, maar dan binnen een rij of kolom.
Een puzzle is opgelost, als het aangegeven vakje (aangegeven met een rondje) is bereikt.

De puzzle hieronder is in één zet op te lossen:

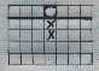Deze puzzle hieronder is in drie zetten op te lossen:
Door de lijn lager te leggen wordt de puzzle moeilijker, zijn er meer
kruisjes nodig voor een oplossing.
Deze puzzle is in vijf zetten op te lossen:
En die hieronder in 6:
En die hieronder in 8:
We vragen ons af:
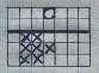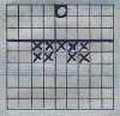zijn er -rekenkundige- criteria op te stellen om bij voorbaat de oplosbaarheid van een
puzzle te bepalen?

We gaan uit van de eindstand.
    X
    0
    0
Die kan het resultaat zijn van:
    0
    X
    X
die is weer ontstond uit:
    000
    0XX
    0XX
die weer ontstond uit:
    00000
    0X0XX
    0X000
    00X00
    00X00
Laten we eens aannemen, dat een X in een vakje een bepaalde hoeveelheid energie vertegenwoordigt.
Stel deze energie gelijk aan "1" in het gele vakje, dat uiteindelijk bezet moet worden.

Stel ook, dat elk vakje minder energie bevat naarmate het verder van het gele vakje af ligt.
Bij elke vakje neemt die energie met een factor p af.
De energie-verdeling ziet er dan zo uit:

    1pp2p3
    pp2p3p4
    p2p3p4p5
    p3p4p5p6
Bij het zetten gaat geen energie verloren, het geslagen X-je draagt zijn energie over.
Dan moet gelden:
    p2 + p = 1 en ook:
    p3 + p2 = p enzovoorts
zodat opgelost moet worden de vergelijking: p2 + p - 1 = 0

Toepassing van de ABC formule levert dan op: p = 0,618033988.

Van elk vakje met een X kan nu de energie worden berekend.
Als de som van deze energiën kleiner is dan 1, dan is geen oplossing mogelijk.