de absolute (abs) functie in Delphi

Gebruik van de absolute functie abs( )

Inleiding

De "system" unit van Delphi bevat de functie abs( x ) waarbij x integer of real kan zijn.
Deze functie levert de absolute waarde van x, dus

Merk op, dat de abs functie 2 functies in zich verenigt:

Dit artikel belicht een paar gevallen waarin gebruik van de abs functie handig is.

1. Afstanden

Stel dat je met de muis aan het tekenen bent. Punten worden op het scherm gezet met muiskliks.
Achtereenvolgende kliks leveren de punten (x1,y1) en (x2,y2) op.
In variabele dx en dy willen we de horizontale en vertikale afstand tussen de punten opslaan.
De code wordt dan

Merk op dat er geen verschil in uitkomst is tussen abs(x1 - x2) en abs(x2 - x1).

Om negatieve afstanden te vermijden kan natuurlijk ook gebruik worden gemaakt van if statements,
maar die zijn trager.
Processoren hebben namelijk een pipeline constructie en bij een if statement moet die pipeline opnieuw
worden opgebouwd.

2. Ondergrens

Stel dat een variabele X nooit negatief mag worden.
Dat wil zeggen : een negatieve X moet omhoog worden afgerond naar 0.
We kunnen weer met een if statement werken, maar met een abs functie kan het ook.

Om dit in te zien is het handig eerst eens de functie y=abs(x) te plotten.

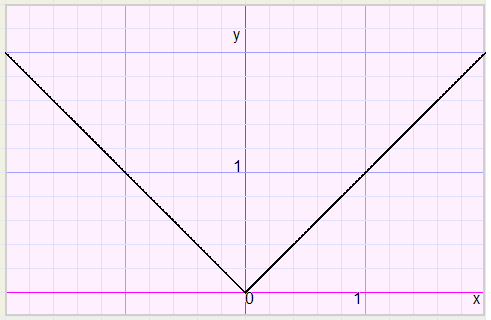
In de grafiek hiervoor heeft een hokje de lengte 0,2.
In het punt (0,0) bevindt zich een knik.
Daarin is de abs functie uniek, want andere functies als, log, sin, cos, tan of polynomen
leveren altijd gebogen grafieken zonder knik.

Alle volgende afleidingen gaan uit van bovenstaande grafiek.
Het knikpunt ligt natuurlijk niet altijd mooi in de oorsprong (0,0).
Daarom eerst een paar trucs om in het algemeen grafieken te verschuiven te spiegelen of uit te rekken.

Als in een willekeurige functie y=f(x) de x wordt vervangen door (x-1)
dan zal de grafiek 1 plaats naar rechts verschuiven.
Ga maar na: stel dat de functie f(x) door punt (p,q) gaat.
Dus q = f(p). Maar als x is vervangen door x-1 dan geldt dus niet meer p = x, maar p = x -1 oftewel x = p + 1.
P is veranderd in p + 1, wat neerkomt op een verschuiving van de grafiek van 1 schaaldeel naar rechts.
Op dezelfde manier is te beredeneren dat vervangen van y door y-1 in y = f(x) de grafiek 1
schaaldeel naar boven verschuift.
X vervangen door x+1 schuift de grafiek 1 plaats naar links, y vervangen door y+1 verschuift de grafiek 1 schaaldeel omlaag.

Als in y = f(x) de x wordt vervangen door x/2, dan rekt de grafiek een factor 2 uit in de x-richting,
dus ten opzichte van de y-as (de y-as heeft als functie x = 0)
Wordt y vervangen door y/2 dan rekt de grafiek in de y richting met een factor 2 uit.

Als in y = f(x) de x wordt vervangen door -x, dan spiegelt de grafiek om de y-as.
Bij vervanging van y door -y spiegelt de grafiek om de x-as.

Met het bovenstaande in gedachten kunnen we het knikpunt overal neerleggen en ook de steilheid aanpassen.
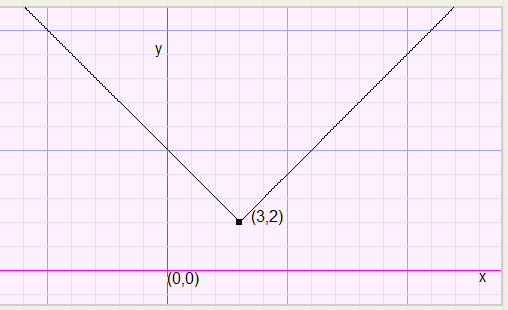
Onderstaande grafiek is dan

Het knikpunt is verlegd van (0,0) naar (3,2)

Voor voor het instellen van een ondergrens van 0, onze doelstelling, combineren we twee functies:
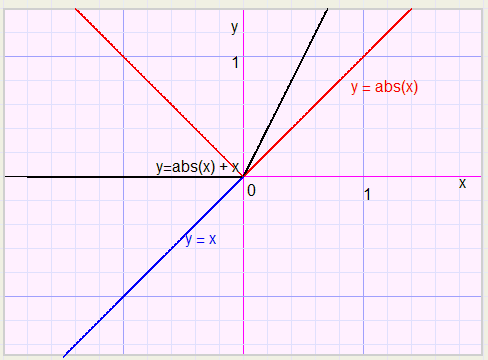
y=abs(x) en y=x.
We plotten de functie y = abs(x) + x

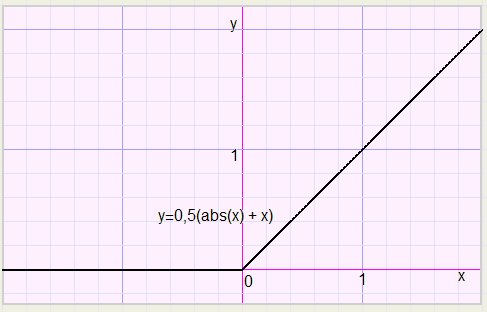
Voor x < 0 levert de functie de gewenste ondergrens van 0, maar vanaf x > 0 is de steilheid 2 keer te groot.
Dat verhelpen we door y te vervangen door 2y, wat de grafiek een factor 2 in vertikale richting laat krimpen.
De functie wordt dan

Stel, dat we voor x een ondergrens van 10 willen.
Het punt (0,0) moet dus worden verschoven naar (10,10).
X vervangen we daarvoor door (x-10) en y door (y-10) zodat

3.Bovengrens

Voor een bovengrens spiegelen we bovenstaande grafiek om de y-as door x door -x te vervangen:

De functie levert de waarde 0 voor x > 0 en abs(x) voor x < 0, niet helemaal de bedoeling.
Nogmaals spiegelen, maar nu om de x- as ( y vervangen door -y)

Nu is voor x > 0 de bovengrens 0 en voor x < 0 geldt y = x.
Het knikpunt is nu naar elk gewenst punt te verschuiven.
De steilheid is aangepast door weer met 0,5 te vermenigvuldigen.

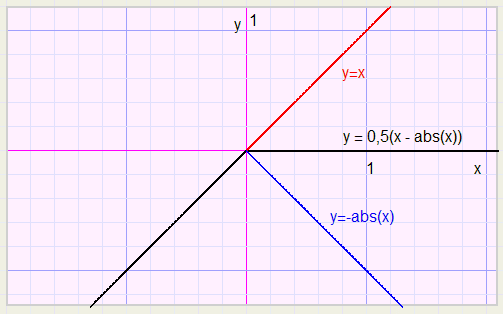
Het punt waar de bovengrens wordt bereikt is x = 0, de bovengrens zelf is ook 0.
Stel dat we x = 100 als bovengrens wensen.
Punt (0,0) moet dan naar (100,100) worden verschoven, wat gebeurt door x te vervangen
door (x-100) en y door (y-100)

4.Onder- en bovengrens

We plotten de functie y = 0,5(abs(x+1) - abs(x-1))
Merk op: een schaaldeel heeft lengte 0,2.

Beneden x = -1 heeft de functie een ondergrens van -1 en voorbij x = 1 is de bovengrens 1

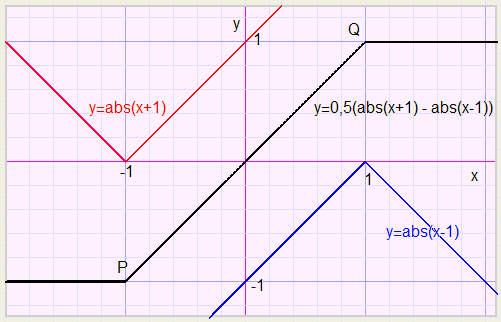
We merken op, dat abs(ondergrens) = abs(bovengrens) = 1

Maar hoe geven we een variabele verschillende onder- en bovengrenzen?
Ga uit van de functie y = 0,5(abs(x+v) - abs(x-v))
Voor x < -v mogen we schrijven:

y = 0,5(-(x+v) - (v-x)) = -v ................ondergrens Voor x > v mogen we schrijven

y = 0,5((x+v) - (x - v)) = v..................bovengrens En voor x > -v & x < v krijgen we

y = 0,5((x+v) - (v-x)) = x ....................geen correctie Stel nu, dat we een ondergrens van a willen en een bovengrens van b.
De afstand tussen de grenzen is b - a.
De bovengrens wordt v = (b-a)/2 en de ondergrens is -v = (a-b)/2.
Absoluut genomen zijn onder- en bovengrens gelijk.
Maar de bovengrens moet niet (b-a)/2 zijn maar b, dus de verschuiving is (eind - begin)

zodat

Zo kan een functie worden gebouwd, die elke gewenste onder- en bovengrens heeft.
En dat zonder gebruik van if statements.
De pipelines van de processor stromen ongehinderd door.
Met mijn grafieken programma Graphics-Explorer is het effect mooi zichtbaar te maken.
Download het programma vanaf http://www.davdata.nl/grxpl.html
Tik in: y = 0,5(abs(x-a) - abs(x-b) + a + b) en klik op "plot".
Selecteer (rechts boven) "vervangen" (niet toevoegen) en "autoplot".
Klik links of rechts op de a en b vakjes om deze constanten te verhogen of te verlagen.
Zo is met muiskliks de onder- en de bovengrens in te stellen. Het resultaat is direct zichtbaar.

Hieronder vat ik de resultaten samen:
Variable x geven we

ondergrens a	met de functie	y = 0,5(abs(x - a) + x + a)
bovengrens b	met de functie	y = 0,5(x - abs(x - b) + b)
beide grenzen a en b	met de functie	y = 0,5(abs(x - a) - abs(x - b) + a + b)

Spectaculair nietwaar?

5.Scheve rechthoeken tekenen

De figuur hieronder toont een bitmap met een 45 graden scheve rechthoek.
De opgave is om deze rechthoek handig te tekenen.

We geven de top pixel de coördinaten (sx,sy)
Zie de figuur hieronder. De zijden van de rechthoek hebben lengtes h en v.
We tekenen de rechthoek door horizontale lijnen te trekken van punt x1 naar x2 op afstand y van de top van de bitmap.

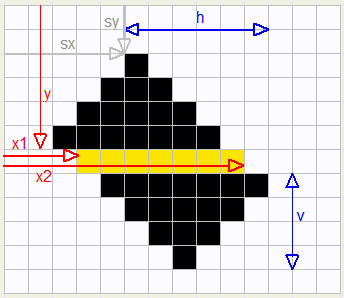
Het programma ziet er dus ongeveer zo uit:

var  j : word;
     h,v : word;
     sx,sy : word;
     bm : Tbitmap;
begin
.....
//creation of bitmap
//setting rectangle dimensions h and v
//setting position (sx,sy)
...
 with bm.canvas do
  begin
   pen.color := 0;
   pen.width := 1;
   for j := 0 to (h-1) + (v-1)     //from top to bottom of rectangle
    begin
     y := sy + j;
     x1 := ???;
     x2 := ???;
     moveto(x1,y);
     lineto(x2,y)
    end;    //for j 
  end;      //with bm
....  
end;

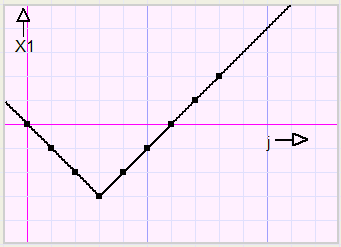
Laten we eens kijken naar het verband tussen x1 en j.
Voor de eenvoud nemen we even aan dat de top de coördinaten (0,0) heeft.

j	0	1	2	3	4	5	6	7	8
x1	0	-1	-2	-3	-2	-1	0	1	2

Van deze tabel maken we een grafiek.
Dat blijkt een geknikte functie te zijn en we herkennen een verschoven
y = abs(x) functie. De verschuiving is 3 in de x- richting en -3 in de y-richting

De functie is dus

Is de hoogte niet 4 maar v dan verandert de functie in ....{3 vervangen door (v-1) }

x1 = abs(j - (v-1)) - (v-1) Voor het eindresultaat moet sx worden opgeteld, dus

x1 = sx + abs(j -(v-1)) - (v-1) Op eendere manier bepalen we een functie voor x2:

x2 = sx - abs(j - (h-1)) + (h-1) + 1
Opmerking:
moveto(0,0) gevolgd door lineto(10,0) tekent een lijn van (0,0) naar (9,0).
Pixel (10,0) wordt niet getekend. Dus moet 1 bij X2 worden geteld.

Hiermee besluit ik dit artikel over toepassingen van de abs( ) functie.