
 |
Cursus Algebra (2) |
| P |
| 2 p |
| 2 | |||||||||
| |||||||||
| p P 2 |
| 4 p 2 |
| P 2 |
| 4 p |
| (+) regel : |
|
bij gelijkblijvende noemers tellers optellen | (*) regel : |
|
teller * teller, noemer * noemer |
| een breuk verandert niet als teller en noemer met hetzelfde getal worden vermenigvuldigd (gedeeld) |
|
delen door een breuk is hetzelfde als vermenigvuldigen met zijn omgekeerde | |||||
|
Breuken gelijknamig maken |
| a |
| 1 |
| 5 |
| 13 |
| 9 |
| 25 |
| 5 |
| 13 |
| 125 |
| 325 |
| 9 |
| 25 |
| 117 |
| 325 |
| 5 |
| 13 |
| 8 x + 1 |
| 4 x − 3 |
| 2 |
| 5 |
| 5 (8 x + 1) + 2 (4 x − 3) |
| 5 (4 x − 3) |
| 40 x + 5 + 8 x − 6 |
| 5 (4 x − 3) |
| 48 x − 1 |
| 5 (4 x − 3) |
| 45 x + 30 |
| 9 x + 6 |
| 15 (3 x + 2) |
| 3 (3 x + 2) |
| c V |
| V + W |
| V (c − d) |
| d |
| 1 |
| d |
| 1 |
| c |
| 1 |
| b |
| 1 |
| a |
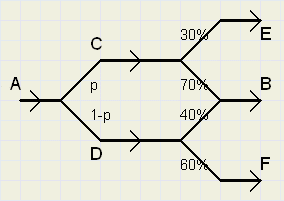 |
| fig.1 |
| a p |
| a q |
| (x 2 + 5 x) 2 |
| (2 x + 10) 2 |
| (x (x + 5)) 2 |
| (2 (x + 5)) 2 |
| x 2 (x + 5) 2 |
| 4 (x + 5) 2 |
| x 2 |
| 4 |
| (x 3 y 5) 6 |
| (x 9 y 15) 2 |
| x 18 y 30 |
| x 18 y 30 |
 "platte" formules
"platte" formules| n − 1 | |||||||||
| |||||||||
| a + 5 |
| b c |
| 5 | ||
3 +
|
 Getallen : Soorten en Toepassing
Getallen : Soorten en Toepassing| soort getal | voorbeelden |
| hoeveelheid | meters, seconden, kilo's, graden Celsius |
| factor | 10%, het dubbele, de helft |
| rangorde | 4 sterren hotel, perron 2A, Willem 3 |
| code | pincode, bus 167, vlucht KL123, ASCII code |
 |
 |
 Afkappen en Afronden
Afkappen en Afronden |
 Neutrale getallen en Inversen
Neutrale getallen en Inversen| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| p |
| q |
| q |
| p |
| 1 |
| 5 x − 3 |
| 3 |
| 7 |
| 17 |
| 7 |
| 7 |
| 17 |
| a |
| b |
| 1 |
| b |
| 1 |
| b |
 Functies
Functies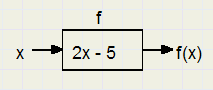 |
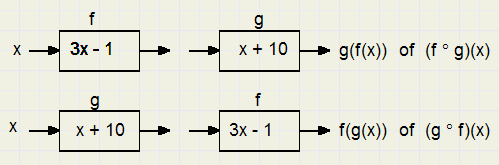 |
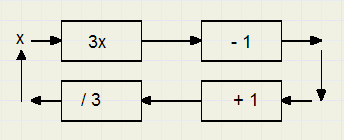 |
| x − 5 |
| 10 − 3 x |
| y − 5 |
| 10 − 3 y |
| 10 x + 5 |
| 3 x + 1 |
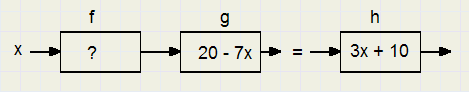 |
| 20 − x |
| 7 |
| 10 − 3 x |
| 7 |
 Verhoudingen
Verhoudingen| a |
| b |
| p a |
| p b |
| 1 |
| 3 |
| 2 |
| 6 |
| 3 |
| 9 |
| y |
| x |
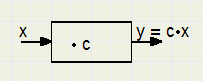 |
| L | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| K | 1,55 | 3,10 | 4,65 | 6,20 | 7,75 | 9,30 | 10,85 | 12,40 |
| p | r |
| q | s |
| q |
| p |
| s |
| r |
 |
| 2,76 | p | 19,86 |
| 9,44 | 84,76 | q |
| t |
| d |
| 2 |
| 3 |
| 3 x |
| 11 x |
| 3 |
| 11 |
| 10 |
| 6 v |
| 10 |
| 7 v |
| 10 |
| 6 v |
| 10 |
| 7 v |
| 1 |
| 12 |
| 10 |
| 42 v |
| 1 |
| 12 |
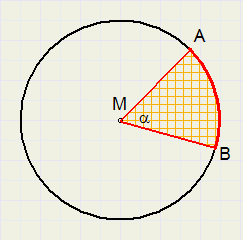 |
| a (graden) | 360 | 1 | a | ||||
| boog AB | 2pr |
|
|
||||
| oppervlakte | pr2 |
|
|
| c |
| x |
| 240 |
| n |
 Gelijkvormigheid
Gelijkvormigheid |
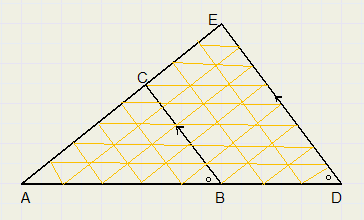 |
| a |
| b |
| a + c |
| b + d |
| c |
| d |
| a |
| b |
 |
 |
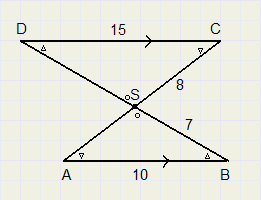 |
| A B.C S |
| D C |
| 10.8 |
| 15 |
| D C.B S |
| A B |
| 15.7 |
| 10 |
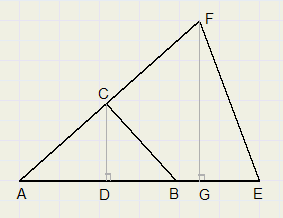 |
| A B.C D |
| A E.F G |
| A B |
| A E |
| C D |
| F G |
| A B |
| A E |
| A C |
| A F |
| A B.A C |
| A E.A F |
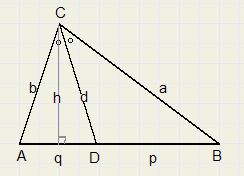 |
| b d |
| a d |
| b |
| a |
| h q |
| h p |
| q |
| p |
 Lineaire Vergelijkingen
Lineaire Vergelijkingen |
 Rekenen met Wortels
Rekenen met Wortels| \ | A |
| \ | A 2 |
| 2 | |||||||
| |||||||
| \ | 49 |
| \ | 100 |
| \ | 10 |
| \ | 2 |
| \ | A |
| \ | B |
| \ | A B |
| = |
|
| \ | A |
| \ | A |
| \ | A |
| \ | A |
| \ | a p |
| p | |||||||
| |||||||
| 2 p | |||||||
| |||||||
| p | ||||||||||||||||
| ||||||||||||||||
| \ | 72 |
| \ | 36 · 2 |
| \ | 36 |
| \ | 2 |
| \ | 2 |
| \ | 500 |
| \ | 100 · 5 |
| \ | 100 |
| \ | 5 |
| \ | 5 |
| \ | x 3 − x 2 |
| \ | x 2 (x − 1) |
| \ | x 2 |
| \ | x − 1 |
| \ | x − 1 |
| \ | 3 |
| \ | 48 |
| \ | 144 |
| = | 5 |
| \ | 3 |
| \ | 12 |
| \ | 3 |
| \ | 3 |
| \ | 3 |
| = |
|
| = |
|
| a |
| b |
| \ | 2 |
| a |
| b |
| a 2 |
| b 2 |
| \ | 2 |
| \ | 2 |
 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| = |
|
| 2 |
| p |
| \ | 2 |
| = |
|
| p 2 + 5 |
| 2 p |
 Haakjes wegwerken
Haakjes wegwerken| 3 v − 8 |
| 5 v + 1 |
| 2 v + 3 |
| 4 v + 1 |
| (3 v − 8) (4 v + 1) − (2 v + 3) (5 v + 1) |
| (5 v + 1) (4 v + 1) |
| 12 v 2 + 3 v − 32 v − 8 − (10 v 2 + 2 v + 15 v + 3) |
| (5 v + 1) (4 v + 1) |
| 12 v 2 − 29 v − 8 − 10 v 2 − 17 v − 3 |
| (5 v + 1) (4 v + 1) |
| 2 v 2 − 46 v − 11 |
| (5 v + 1) (4 v + 1) |
| æ |
| ö | | |
| è | ø |
| a + b |
| a − b |
| a + b |
| b |
| a − b |
| a + b |
| a − b |
| b |
| = |
|
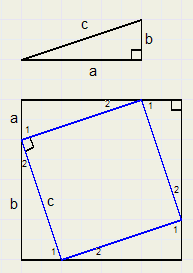 |
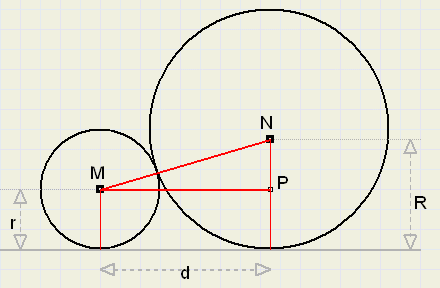 |
| \ | R.r |
 Ontbinden in factoren
Ontbinden in factoren| x 2 − 1 |
| (x + 1) 2 |
| (x − 1) (x + 1) |
| (x + 1) 2 |
| x − 1 |
| x + 1 |
| 25 x y 2 + 60 x y + 36 x |
| 10 x y + 12 x |
| x (25 y 2 + 60 y + 36) |
| 2 x (5 y + 6) |
| (5 y + 6) 2 |
| 2 (5 y + 6) |
| 5 y + 6 |
| 2 |
| x 8 − 1 |
| x 4 − 1 |
| (x 4 − 1) (x 4 + 1) |
| x 4 − 1 |
| (15 x − 20 y) (15 x + 21 y) |
| (9 x − 12 y) (25 x + 35 y) |
| 5 (3 x − 4 y) · 3 (5 x + 7 y) |
| 3 (3 x − 4 y) · 5 (5 x + 7 y) |
| 1. 50 | 1 + 50 = 51 |
| 2 . 25 | 2 + 25 = 27 |
| 5 . 10 | 5 + 10 = 15 |
| -1. 63 | -1 + 63 = 62 |
| -3.23 | -3 + 23 = 20 |
| -7 . 9 | -7 + 9 = 2 |
| 7 . -9 | 7 - 9 = -2 |
| x 2 − 6 x − 91 |
| x 2 − 6 x − 7 |
| (x + 13) (x − 7) |
| (x − 7) (x + 1) |
| x + 13 |
| x + 1 |
| 3 |
| p 2 − p − 2 |
| 2 |
| p 2 + 4 p + 3 |
| 4 |
| p 2 + p − 6 |
| 3 |
| (p − 2) (p + 1) |
| 2 |
| (p + 1) (p + 3) |
| 4 |
| (p + 3) (p − 2) |
| 3 (p + 3) + 2 (p − 2) + 4 (p + 1) |
| (p + 1) (p − 2) (p + 3) |
| 9 (p + 1) |
| (p + 1) (p − 2) (p + 3) |
| 9 |
| (p − 2) (p + 3) |
| 10 |
| 2 x − 11 |
 |
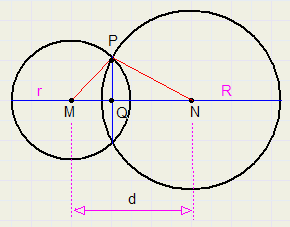 |
| R 2 − r 2 + d 2 |
| 2 d |
| \ | a |
| 2 | |||||||
| |||||||
| 2 | |||||||||
| |||||||||
| 2 |
| p |
| 2 | |||||||||
| |||||||||
 De Zwaartelijn Formule
De Zwaartelijn Formule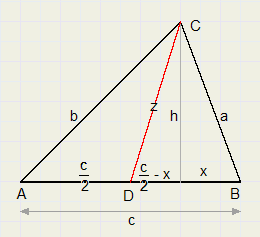 |
| a 2 + c 2 − b 2 |
| 2 c |
| 2 | |||||||||
| |||||||||
| 4 a 2 c 2 − (a 4 + a 2 c 2 − a 2 b 2 + a 2 c 2 − b 2 c 2 + b 4 − a 2 b 2 − b 2 c 2 + b 4) |
| 4 c 2 |
| 2 a 2 c 2 + 2 a 2 b 2 + 2 b 2 c 2 − a 4 − b 4 − c 4 |
| 4 c 2 |
| 2 a 2 c 2 + 2 a 2 b 2 + 2 b 2 c 2 − a 4 − b 4 − c 4 |
| 4 c 2 |
| 2 | |||||||||||
| |||||||||||
| 2 a 2 c 2 + 2 a 2 b 2 + 2 b 2 c 2 − a 4 − b 4 − c 4 + (b 2 − a 2) 2 |
| 4 c 2 |
| 2 a 2 c 2 + 2 b 2 c 2 − c 4 |
| 4 c 2 |
| 2 a 2 + 2 b 2 − c 2 |
| 4 |
 Test
Test| 2 a 2 |
| a + 3 |
| æ |
| ö | | | ||||
| è | ø |
| x 2 − 3 x − 28 |
| x 2 − 9 x + 14 |
| 3 x − 15 |
| 3 x + 27 |
| 5 x − 45 |
| 5 x + 25 |
| (6 k 6 m 5) 2 |
| 9 k 10 m 7 |
| ||
k 2
|
 |
 |

 Klik [hier]
voor een e-mail bericht met uw
Klik [hier]
voor een e-mail bericht met uw