Bierkratten Stapelen In het Noord-Hollandse dorp Limmen is op 12-06-2005 het wereldrecord bierkratten-stapelen gebracht op 63365. Bij het lezen van zo'n bericht vraag je je af of dat getal wel klopt. En hoeveel lagen die piramide dan wel bevat. Of hoeveel kratten er nodig zijn om 1,2,3,...,n lagen te stapelen. In dit artikel wordt een formule voor het aantal kratten afgeleid, als het aantal lagen (n) bekend is. Deze formule wordt experimenteel verkregen. Voor het bewijs dat deze formule altijd klopt, ook voor zeer grote getallen, wordt een zg. bewijs met "Volledige Inductie" gebruikt. Tenslotte wordt de formule nog toegepast om een formule voor de inhoud van een piramide te vinden. Daarbij wordt het begrip "limiet" gebruikt. Om te wennen aan de manier van redeneren vooraf een eenvoudiger voorbeeld : een piramide waarin de kratten 1 laag dik zijn gestapeld. Een formule voor de som van oplopende termen 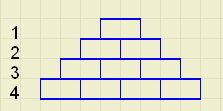Een piramide met n lagen bevat 1 + 2 + 3 + .... + n kratten. Het aantal kratten in laag n noemen we tn, dus: t1 = 1 t2 = 2 tn = n Het totale aantal kratten in lagen 1 + 2 + 3 + .... + n noemen we Sn, dus S1 = t1 = 1 S2 = t1 + t2 = 1 + 2 = 3 S3 = t1 + t2 + t3= 1 + 2 + 3 = 6 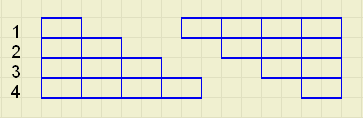Gevraagd: een formule voor Sn Eerst een meetkundige oplossing: Maak twee gelijke stapels, schuif de kratten naar links en draai 1 stapel 180 graden. De stapels van 4 lagen vormen dan een rechthoek van 4 * 5 = 20 kratten. Het aantal kratten in 1 stapel is de helft, dus 10 kratten. Als er n lagen zijn, dan ontstaat op deze manier een rechthoek van n(n+1) kratten zodat: Sn =  n (n + 1) 2 Voorbeeld: Voor een piramide van 50 hoog zijn dus 50(50+1)/2 = 1275 kratten nodig. We leiden nu dezelfde formule op een andere, experimentele, manier af. In een tabel schrijven we n op rij 1 en Sn eronder op rij 2. Dan voegen we rijen toe, waar Sn wordt gemanipuleerd met als doel per kolom dezelfde uitkomst te krijgen. Merk op, dat we intuïtief te werk gaan en het heel wat gepruts kan kosten om een resultaat te verkrijgen. n 1 2 3 4 5 6 Sn 1 3 6 10 15 21 Sn n 1 1,5 2 2,5 3 3,5 2 Sn n 2 3 4 5 6 7 2 Sn n (n + 1) 1 1 1 1 1 1 zodat 2 Sn n (n + 1)  = 1 en Sn =  n (n + 1) 2 De gevonden formule klopt natuurlijk voor n=1,2,3,4,5 maar daarna zijn we niet zeker. Het bewijs, met volledige inductie, wordt nog even bewaard. Eerst zoeken we een formule voor de ruimtelijke piramide. Een formule voor de som van oplopende kwadraten Terug naar Limmen met de ruimtelijke piramide van bierkratten. De bovenste laag bevat 1 krat, die eronder 2*2 = 4 en daaronder 3*3 = 9 kratten. Het aantal kratten in laag n noemen we tn, dus: t1 = 1 t2 = 4 t3 = 9 tn = n2 Het totale aantal kratten in lagen 1 + 2 + 3 + .... + n noemen we Sn, dus S1 = t1 = 1 S2 = t1 + t2 = 1 + 4 = 5 S3 = t1 + t2 + t3= 1 + 4 + 9 = 14 We zoeken een formule Sn = 1 + 4 + 9 + 16 + ....+ n2 en maken een tabel als hiervoor en manipuleren opnieuw Sn. Dat kost heel wat moeite, maar alleen het resultaat wordt weergegeven, niet de bergen kladpapier die zijn verbruikt. n 1 2 3 4 5 6 n2 1 4 9 16 25 36 Sn 1 5 14 30 55 91 6Sn 6 30 84 180 330 546 6 Sn n 6 15 28 45 66 915 6 Sn n (n + 1) 3 5 7 9 11 13 6 Sn n (n + 1) (2 n + 1) 1 1 1 1 1 1 zodat: Sn =  n (n + 1) (2 n + 1) 6 Vullen we voor n in 57, de hoogte van de piramide, dan is Sn = 63365, de Limmenaren spreken dus de waarheid. Merk op, dat we er niet zeker van zijn, dat de formule ook voor grote waarden van n klopt. Tijd om dat te bewijzen. Maar om de methode te demonstreren, eerst de aanpak voor de "platte" piramide. De hierna volgende methode om de juistheid van een experimenteel verkregen formule te bewijzen heet een bewijs met "volledige inductie". Volledige inductie Het principe van volledige inductie luidt als volgt: Laat Sn een formule (of bewering) zijn over de variabele n. We bewijzen dat: 1. S1 klopt 2. Als Sn klopt voor n = k, dan klopt Sn ook voor n = k + 1. Is aan deze voorwaarden voldaan dan volgt uit S1 de juistheid van S2, uit S2 volgt S3 ...enzovoorts. Dus Sn klopt voor alle waarden van n. We bewijzen eerst de juistheid voor de platte piramide Sn =  n (n + 1) 2 1. S1 = 1.2/2 = 1 , klopt. 2. Stel dat de formule juist is voor n = k, Sk =  k (k + 1) 2 Haakjes en breuk wegwerken: 2Sk = k2 + k Nu is Sk+1 = Sk + (k+1) of: 2Sk+1 = 2Sk + 2(k+1) = k2 + k + 2(k+1) = k2 + 3k + 2 Sk+1 is ook te verkrijgen door (k+1) in te vullen voor n in de formule voor Sn: 2Sk+1 = (k+1)((k+1)+1) = k2 + 3k + 2 We zien: Om Sk+1 te vinden levert invullen van k+1 in de formule Sn hetzelfde resultaat op als de berekening Sk+1 = Sk + k+1 Aangezien S1 klopt, is dus de formule ook correct voor n=2, maar dan ook voor n=3,4,5... Hiermee is de "platte piramide" formule bewezen. De ruimtelijke piramide-formule gaat op eendere wijze, maar is iets meer rekenwerk. We stellen vast, dat Sn =  n (n + 1) (2 n + 1) 6 klopt voor n = 1. Stel dat de formule klopt voor n = k Sk =  k (k + 1) (2 k + 1) 6 Haakjes en breuk wegwerken : 6Sk = 2k3 + 3k2 + k Aangezien Sk+1 = Sk + (k+1)2 is 6Sk+1 = 2k3 + 3k2 + k + 6(k+1)2 = 2k3 + 3k2 + k + 6k2 + 12k + 6 = 2k3 + 9k2 + 13k + 6 We proberen dit laatste resultaat ook te krijgen door (k+1) in te vullen voor n in 6Sn = n(n+1)(2n+1) 6Sk+1 = (k+1)(k+2)(2k+3) = (k+1)(2k2 + 7k + 6) = 2k3 + 9k2 + 13k + 6, hetzelfde antwoord als hiervoor. Ook deze formule is dus correct voor alle waarden van n Nog een voorbeeld van Volledige Inductie We bewijzen, dat an - 1 deelbaar is door (a-1). Stap 1. : dat klopt voor n = 1 Stap 2. : stel dat ak - 1 deelbaar is door (a-1) Nu is ak+1 - 1 = ak+1 - a + a - 1 = a(ak - 1) + (a - 1), wat dan ook deelbaar is door (a-1) De bewering klopt dus voor alle waarden van n. Opmerking: In het a-tallig stelsel is an - 1 een getal met alleen de cijfers (a-1). Na deling door (a-1) heeft het getal de vorm 111...111111. Voor wie zelf aan de slag wil met Volledige Inductie hier een paar (bekende) gevallen: bewijs dat a. 1 + 4 + 7 + ... + (3n-2) = 3 n 2 − n 2 b. 13 + 23 + .. + n3 = (1 + 2 + 3+ ....+ n)2 c. 5n - 4n - 1 is deelbaar door 16 Limieten Stel eens, dat we van A naar B lopen en AB = 1 meter. We bewegen ons echter wat vreemd voort: met elke stap halveren we onze afstand tot B. Zodoende leggen we in stapjes de afstand 1 2  +  1 4  +  1 8  +  1 16  +  1 32 af. Het zal duidelijk zijn, dat we B nooit bereiken, maar ook, dat we B zo dicht mogelijk kunnen benaderen als we maar willen. Voor zo'n onbereikbaar maar toch zo nabij doel is een notatie bedacht: lim ( 1 2  +  1 4  +  1 8  +  1 16  +  1 32 .....) = 1 lim is een afkorting van "limiet" , dat is dus het getal dat wordt benaderd. Let op: de limiet in bovenstaand voorbeeld is dus niet ongeveer maar precies gelijk aan 1. Een veel gebruikte limiet is: lim 1 x x → +¥  = 0 Deze limiet gaan we gebruiken om uitgaande van de "piramide-formules" de formules af te leiden voor de oppervlakte van een driehoek en de inhoud van een piramide. De oppervlakte van een driehoek (maar dan even anders...) 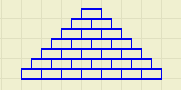We gebruiken zeer kleine kratten met lengte a en hoogte h. Die worden n lagen hoog gestapeld, waarbij n zeer groot is. De piramide zal dus de vorm van een driehoek benaderen. De oppervlakte O van de (trapvormige) driehoek is dus: O = n (n + 1) 2  a h Als de basis van de driehoek A is, dan A = an of a =  A n en ook, als de hoogte H is : h =  H n invullen levert: O =  n (n + 1) 2  ·  A n  ·  H n = H A 2  +  H A 2 n Deze laatste term nadert tot 0 voor zeer grote waarden van n, zodat O = H A 2 basis * hoogte gedeeld door 2. Op eenzelfde manier kan, uitgaande van de formule Sn = 1 6  n (n + 1) (2 n + 1) worden bewezen, dat de inhoud I van een piramide gelijk is aan I = 1 3  G H , waarbij G de oppervlakte is van het grondvlak en H de hoogte. Het rekenwerk wordt aan de lezer overgelaten.