Biljarten

Download biljart programma.

Download complete Delphi-7 project.

Dit artikel gaat over een simpel biljartspel:
de fysica van botsende ballen gesimuleerd met een Delphi programma.

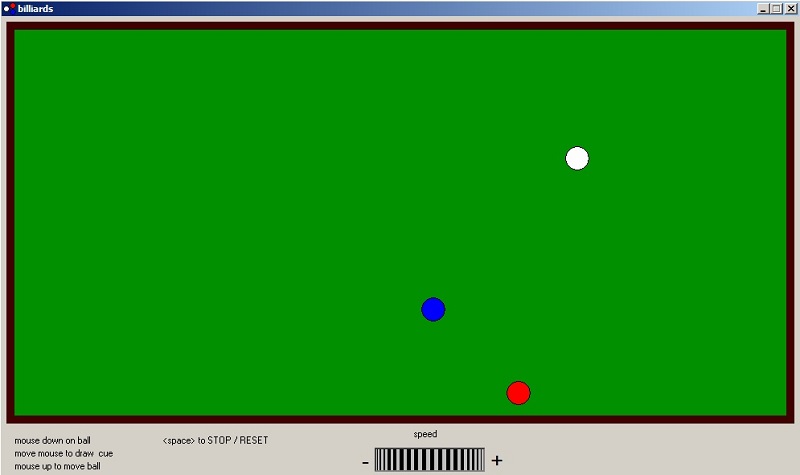
Wat kan je met het programma?

Een bal in beweging zetten:

Ballen stilzetten:

Twee keer de spatiebalk indrukken zet de ballen in hun oorspronkelijke positie.
Om de snelheid van de ballen te wijzigen:

Dit project dient om de balbewegingen te simuleren, niet om een spelletje te biljarten.
De ballen stoppen niet met bewegen wat niet erg realistisch is maar wel heel levendig.
Met weinig extra moeite is er wel een echt biljartspel van te maken:

Botsende ballen

We veronderstellen zogenaamde "elastische" botsingen.
Dat betekent dat een bal bij botsing tijdelijk iets wordt ingedrukt maar niet permanent van vorm verandert.
Er gaat geen energie verloren.

1. Botsen tegen de kant
Als een bal tegen de kant botst dan drukt de rand wat in.
Daardoor ontstaat een kracht tegengesteld aan de beweging.
Eerst vertraagt de bal om dan in de tegenovergestelde richting te versnellen.

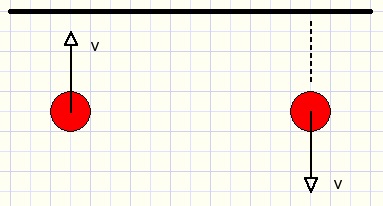
In het plaatje hierboven is v de snelheid van de bal.
De bewegingsrichting is loodrecht op de rand.
In geval van andere richtingen moet de snelheid worden ontbonden in een horizontale- en een vertikale component.
Na de botsing is de balsnelheid de vectorsom van de horizontale- en de omgekeerde vertikale snelheid.

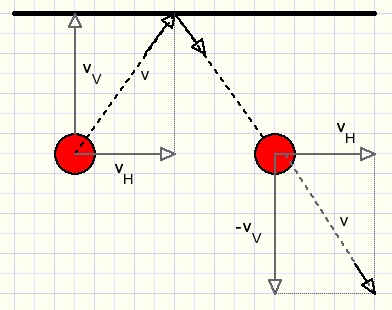
2.Botsingen tussen twee ballen.
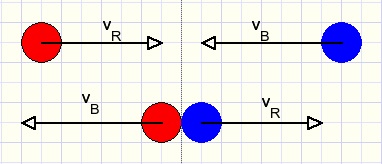
Eerst de situatie waar één bal stilstaat.
In het plaatje hieronder raakt de rode bal de stilstaande blauwe.
De bewegingsrichting is naar het middelpunt.
De rode bal vertraagt maar dezelfde kracht versnelt de blauwe bal.
Als de rode bal stilstaat beweegt de blauwe met dezelfde snelheid verder.

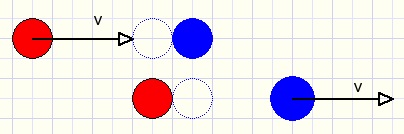
Nu de situatie waarin beide ballen verschillende snelheid hebben.
Stel hun snelheden zijn V_r en V_b en dat V_r = V_b + x.
Als x = 0 dan botsen de ballen om daarna in omgekeerde richting te bewegen met dezelfde snelheid.
Als de rode bal de stilstaande blauwe raakt met snelheid x,
dan zagen we al dat de blauwe bal de snelheid van de rode overneemt.
Deze bewegingen optellend zien we dat de rode bal beweegt met snelheid V_b
en de blauwe bal met snelheid (V_b+x).
De ballen verwisselen simpelweg van snelheid.

Beweging in willekeurige richtingen
Denk aan een lijn die de middelpunten van de ballen verbindt.
De balsnelheden moeten worden ontbonden in componenten in de richting van die lijn tussen de middelpunten
en de richting loodrecht daar op.
Opnieuw: de ballen verwisselen hun snelheid in de richting van de middelpuntslijn.

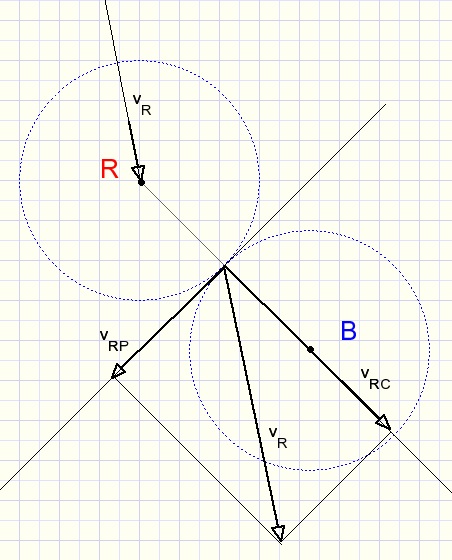
In het plaatje hierboven is alleen de snelheid van de rode bal ontbonden om onduidelijkheid te voorkomen.
De snelheid van de blauwe bal ontbinden we in componenten v_BC en v_BP
Na botsing zijn dan de snelheden van de ballen:

_BC

_RP

_RC

_BP

Bewegingsrichting

De snelheid is aangegeven met een positief getal.
De richting staat in radialen:

Merk nog op, dat in het coördinatenstelsel de positieve (vertikale) Y richting omlaag is.
In het kwadrant rechtsonder zijn dus zowel x als y positief.
De balbeweging met poolcoördinaten aangevend is de snelheid altijd positief
en de hoek geeft de richting aan.

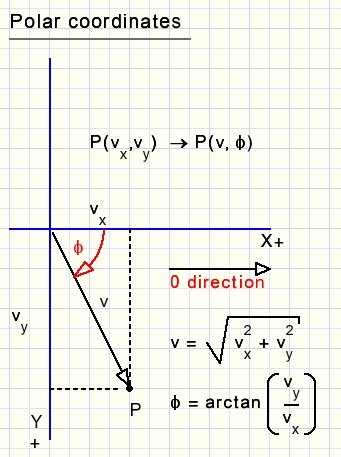
Hierboven staat de omzetting van Cartetische- naar poolcoördinaten.
Een snelheid ontbinden in twee loodrecht op elkaar staande richtingen is simpel:

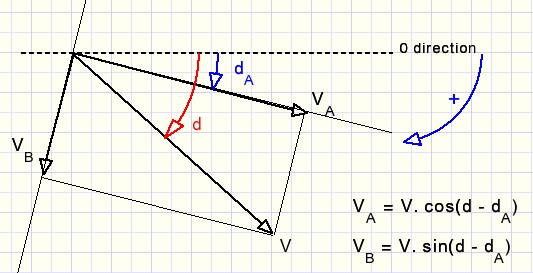
d is de richting in radialen. Hoeken nemen toe bij draaiing met de klok mee.
Andere richtingen gaan vanzelf goed omdat de sinus en cosinus functies in andere kwadranten
het juiste teken verschaffen.
Eén probleem blijft over: de arctangens functie ziet geen verschil tussen diagonaal liggende kwadranten.
Die geeft altijd een hoek tussen -p/2 en p/2

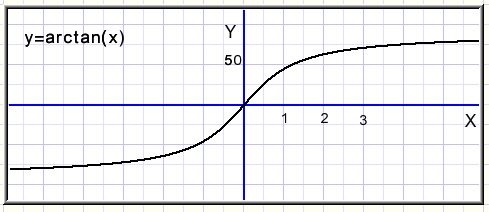
In de grafiek hierboven staat de hoek in graden.
De volgende functie verschaft wel de juiste richting:

function XYdirection(x,y : single) : single;
//geef richting (0,0) naar (x,y) in radialen (-pi .. + pi)
const pi05 = 0.5*pi;
begin
 if x = 0 then
  begin
   if y < 0 then result := -pi05 else result := pi05;
  end
  else begin
        result := arctan(y/x);
        if x < 0 then
         if y < 0 then result := result - pi
          else result := result + pi;
       end;
end;

Het Delphi programma

data formats.

const balldiameter = 30;
      ballradius = balldiameter * 0.5;
      speed = 0.25;  //pixels per step
      pi05 = pi*0.5;
      pi2  = pi*2;

type TBallcolor = (Redball,whiteball,blueball,noBall);
     TBall = record
              xpos : single;  //x coordinate of ball center
              ypos : single;  //y ..
              vel  : single;  //velocity
              dir  : single;  //direction
             end;

var bm : TBitmap;
    ballmap : array[redBall..blueBall] of Tbitmap;
    ball : array[redBall..blueBall] of TBall;
    eraseBall : TBitmap;
    moving,drawing : boolean;
    x1,y1,x2,y2 : smallInt;
    selected : TBallColor;

Bitmap (BM) heeft afmetingen 960*480 pixels, hetzelfde als paintbox1 op het form.
De randen zijn getekend op het canvas van het form, rondom de paintbox.

Voor elke bal is er een transparante bitmap.
Bij het starten wordt de inhoud eenmalig getekend.
De eraseMap is geheel groen en dient om ballen te wissen.

Nauwkeurigheid

Een bal start steeds met een snelheid van 0.25 pixels per stap.
Dat is de maximum snelheid.
Na elke stap wordt gekeken of er overlapping is ontstaan met een rand of een andere bal.
Kleine stapjes geven een nauwkeuriger positie van de botsing.
Na elke 8 stapjes wordt het scherm bijgewerkt om de nieuwe balposities weer te geven:

Timing

De computer heeft een milliseconden klok: functie gettickcount
levert het aantal milliseconden na het aanschakelen van de computer.
Probleem is dat deze klok ongeveer eens per 16 milliseconden wordt bijgewerkt.
Dat is veel te traag.

Een andere klok loopt op CPU snelheid.
Die gaan we gebruiken.
Processoren zijn er in verschillende snelheden zodat conversie nodig is
van de CPU klok naar de echte tijd.
Met dat laatste helpt procedure GetCPUticks die het aantal klokcycli geeft per microseconde.
Een 3GHz klok levert dus de waarde 3000.
Functie CPUtime geeft de CPU tijd in een 64 bit integer: het aantal klokcycli sinds inschakeling.

Voor de instelling van de balsnelheid is een rotation button toegevoegd onder de biljarttafel.
Deze knop is een zelfgemaakt component maar om de lezer niet te ontrieven heb ik de code toegevoegd
in een aparte unit zodat er geen vreemde componenten geïnstalleerd hoeven te worden.

De rotatie knop levert waarden tussen 0 en 100.
Daarmee bepalen we de tijd tussen het bijwerken van de balposities.

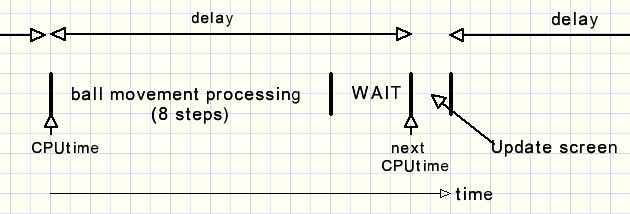
De berekeningen van de nieuwe balposities vergt ongeveer 500 microseconden per 8 stappen. (bij een 3Ghz klok)
Delay waardes moeten variëren van 1000 tot 10000 microseconden.
De delay waarde wordt relatief verhoogd, dus met steeds een vermenigvuldigfactor.

100 - buttonposition omdat een hogere waarde een kortere delay waarde moet opleveren.
variabele nextCPUtime = CPUtime + CPUticks * delay.

Bal beweging

Bij elke stap verandert de positie van een bal met zijn snelheid.
Eerst wordt gekeken of overlapping met een rand plaatsvindt.
Daarna vindt controle plaats op overlapping tussen rood/wit, rood/blauw of wit/blauw.
Procedure collision(a,b : TBallColor) voert die tests uit en berekent de nieuwe richting en snelheid van de ballen.

betekenis van de variabelen in procedure collision(a,b : TBallcolor)

xA	bal a X coördinaat
yA	bal a Y coördinaat
xB,yB	bal b idem...
dA	bal a richting
vA	bal a snelheid, altijd positief
dB,vB	bal b idem...
d	afstand tussen middelpunten van de ballen a,b
dCC	richting van de lijn tussen de middelpunten
vAC	bal a snelheid in richting van de lijn door middelpunten (+ or -)
vAP	bal a snelheid in richting loodrecht op vAC (+ or -)
vBC,vBP	bal b idem...

Voor details verwijs ik naar de voorgaande theorie en de source code.

OneStat