Bladwijzer vouwen

Inleiding

Reizigers gebruiken hun reis- of wachttijd vaak om een boek te lezen.
Veel van die boeken hoeven niet te worden bewaard en er is dus geen reden om er zuinig mee om te gaan.
Het boek zal zelden in één aaneengesloten periode worden uitgelezen.
Daarom dient te worden aangegeven tot welke bladzijde de lezer in het boek is gevorderd.
Dat kan op een paar manieren:
    1.de gelezen bladzijden worden uit het boek gescheurd (aan te bevelen voor wandelaars)
    2. na de laatst gelezen pagina wordt een bladwijzer ingeklemd (nadeel: die kan wegraken)
    3. de laatst gelezen bladzijde wordt naar binnen gevouwen, zodat een driehoekje uitsteekt
In dit artikel kiezen we voor methode 3.

Het probleem

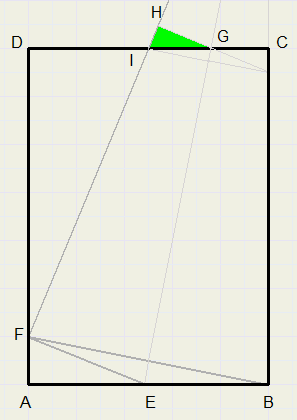Bekijk eens het plaatje hiernaast.
Bij het vouwen van een bladzijde ontstaat aan de bovenzijde een driehoekje,
dat uitsteekt.
Hoe moet worden gevouwen om de oppervlakte van dit driehoekje
zo groot mogelijk te maken?
Oftewel, hoe groot maken we lengte AF
bij gegeven breedte en hoogte van een bladzijde?

Merk op:
EG is de vouwlijn.
Punt B vouwt over F, C wordt H.

BE = EF
CG = GH

Aanpak

Bij dit probleem loert het gevaar in oeverloze berekeningen te verzanden.
Het is dus zaak om eerst de strategie goed vast te leggen.

We vermoeden dat we de Stelling van Pythagoras nodig hebben en verder
gebruik zullen maken van gelijkvormige driehoeken.
We verlengen zijde BC en vouwlijn EG om driehoeken te maken.
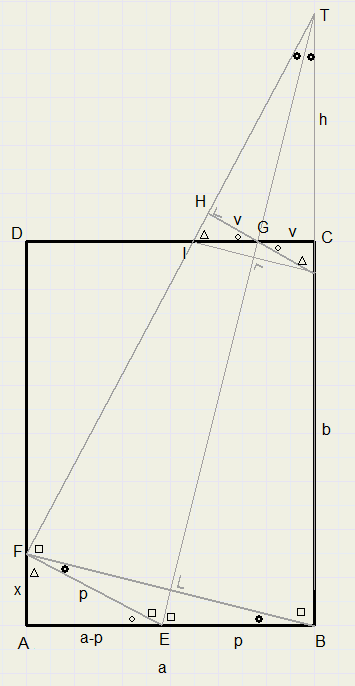Voor het gemak stellen we
    AB = a
    BC = b
    AF = x
    BE = EF = p
    TC = h
    CG = GH = v
Gelijk gemerkte hoeken zijn gelijk.
Met F,Z,X hoeken en symmetrie is dat in te zien.

Uiteindelijk doel is een formule,
die de oppervlakte van driehoek GHI
uitdrukt in x,a en b.

Het teken ~ betekent gelijkvormigheid.
Het teken @ betekent gelijkheid (congruentie).
De oppervlakte van driehoek GHI schrijven we als [GHI]

De Strategie

p is te berekenen uit a en x.
DTBE ~ DBAF, dus h kan berekend worden
DTCG ~ DTBE, dus v kan berekend worden

DGHI ~ DEAF
Als f = v : AE, dan is
[GHI] = f2[EAF],
want de oppervlakten van gelijkvormige driehoeken
verhouden zich als de kwadraten van twee
overeenkomstige zijden.

Berekening van p

Stelling van Pythagoras in DEAF



Berekening van h

DTBE ~ DBAF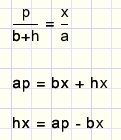



Berekening van v

DTCG ~ DTBE



vermenigvuldigen met x



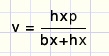
hx vervangen ap - bx



Berekenen van f





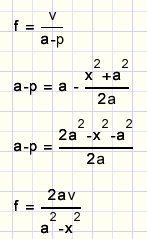
v invullen:




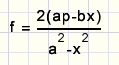
p invullen en formule vereenvoudigen



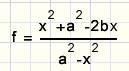
De oppervlakte van driehoek GHI

    [GHI] = f2[EAF]
    [GHI] = f2x(a-p)/2
    f, a-p invullen en vereenvoudigen


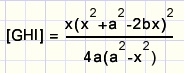
Voor x=0 is ook de oppervlakte 0, dat klopt.
x=a is onmogelijk.
Bij vouwlijn CE zien we dat p:b = x:a, dus ap = bx, zodat f = 0

De maximale oppervlakte

Differentiëren is weinig aantrekkelijk, want de afgeleide zal een vijfdegraads functie zijn.
We voeren de formule aan Graphics-Explorer, waarbij we de oppervlakte y noemen
    y = x(x^2+a^2-2b*x)^2 / (4a(a^2-x^2))
en we maken a = 12 en b = 16
Ook selecteren we autoplot en vervangen
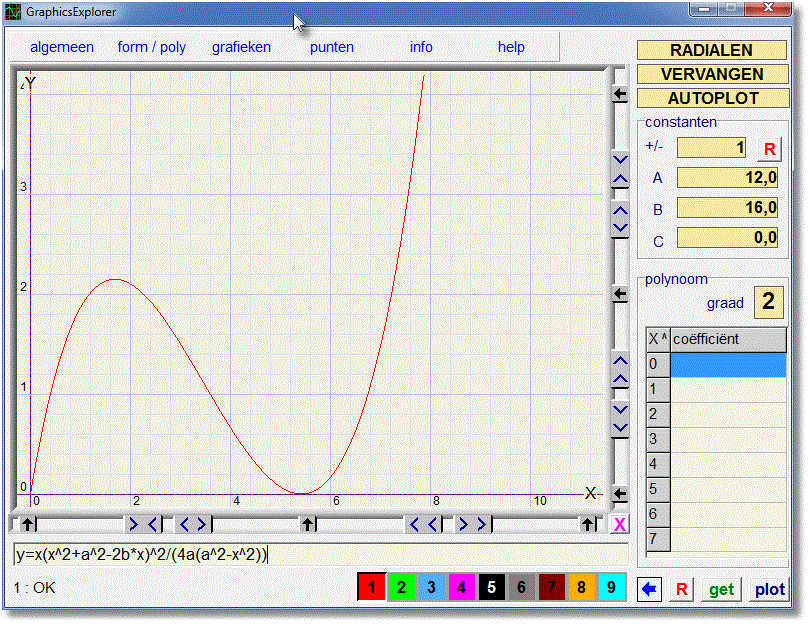
De grafiek toont y = 0 voor x=0 en ook voor x= 5,44
Het maximum treedt op voor x = 1,72