

| Een telwerk voor combinaties |  |
Voor de theorie van permutaties en combinaties: kijk [hier]
Wat is een combinatie?
Stel we moeten uit een groep van 10 personen er 3 kiezen voor corvee.Een keuze heet een combinatie.
De volgende vragen rijzen:
-
1.hoeveel keuzen zijn er mogelijk?
2.wat is de volgende keuze gegeven de vorige?
Even in het kort wat theorie.
10 objecten kan je op 10.9.8.7.6.5.4.3.2.1 = 10! manieren op een rijtje zetten.
10! is een verkorte schrijfwijze, spreek uit : tien faculteit.
De letters van het woord torenflat zijn op 9! manieren op een rijtje te zetten.
Maar neem nu het woord zeemleer.
De letters e zijn het probleem.
Maak dus eerst de e's verschillend, bijvoorbeeld door ze een aparte kleur te geven.
Dan zijn de letters op 8! manieren op een rijtje te zetten.
De e's zijn op 4! manieren op een rijtje te zetten, zodat 8! dus 4! maal te groot is.
Met het woord zeemleer kunnen we dus 8!/4! verschillende "woorden" maken.
Terug naar de corveeploeg.
We kozen 3 personen uit 10.
Dat doen we door ze een bordje op te spelden met Y voor gekozenen en N voor afgewezen personen.
De vraag wordt hiermee: hoeveel "woorden" kan je maken van de letters YYYNNNNNNN ?
Dat is 10! / (3! . 7!)
Immers, 10! is het aantal volgorden als alle letters verschillend zijn.
Maar de Y's zijn op 3! en de N's op 7! manieren op een rijtje te zetten.
Daar moet door worden gedeeld.
Het vorige voorbeeld noemen we : "de combinaties van 3 uit 10".
Ook wel geschreven als C(10,3) = 120.
Algemeen bij K keuzen uit N objecten:
-
C(N,K) = N!/(k!.(N-K)!)
Het programma
Hieronder een plaatje van het programma in werking: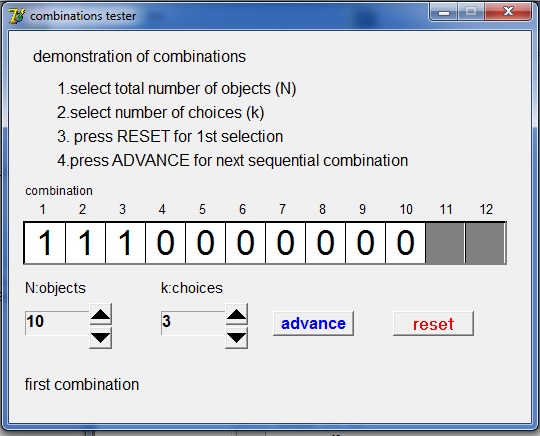
De objecten zijn hier de bit posities (1..10).
Een "1" wil zeggen: gekozen, een "0": niet gekozen.
Het plaatje toont de eerste combinatie van 3 uit 10 personen, namelijk de keuze 1,2,3.
De volgende combinatie is logischerwijze: 1,2,4.
Dat gaat zo door tot 1,2,10 en daarna komt 1,3,4......1,3,5.........enzovoorts.
Door op de advance knop te drukken verschijnt steeds de volgende combinatie.
De programma code
Er zijn UP_DOWN tellertjes om het aantal objecten N in te stellen en het aantal keuzes K.Het maximale aantal objecten is 12.
De variabelen in het programma heten ook N en K.
De combinatie wordt getoond in een paintbox en staat in een word (bits 1..12).
(bit 1 = 1 als object 1 werd gekozen , enz.)
Deze word variable heet SH (van shifter)

Van het word SH worden bits 0 en 13,14,15 niet gebruikt.
RESET
Deze procedure genereert in SH een rijtje van K "1" bits, te beginnen met bit 1.Merk op dat het word omgekeerd wordt weergegeven: de lagere bits links.
Dat werkt wat prettiger, van links naar rechts.
procedure resetSH;
//set SH to first combination of K out of N
var i : byte;
mask : word;
begin
SH := 0;
mask := 1;
for i := 1 to K do
begin
mask := mask shl 1;
SH := SH or mask;
end;
end;
advanceSH
advanceSH is een functie, die true afgeeft bij een volgende combinatieen false als de laatste combinatie is bereikt.
Deze functie is wat lastiger dan de vorige.
In unit1 zien we nog deze constante en variabelen:
const maxN = 12;
var N,K : byte; //K choices out of N objects
SH : word;
timercode : byte;
Om niet herhaald op knopjes te moeten drukken is een timer aangebracht.Die zorgt voor herhaalde actie zolang een knop blijft ingedrukt.
De timercode bepaalt de actie die de timer moet uitvoeren.
Zie de source code voor details.
function advanceSH : boolean;
//SH shift counter increment
//return true if advanced
//use N,K
var count,pos,i : byte;
mask : word;
Done : boolean;
begin
result := false;
count := 0;
pos := N;
Done := false;
repeat
mask := (1 shl pos);
if SH and mask > 0 then //test SH bit
begin
SH := SH xor mask; //remove 1
inc(count); //count removed 1
if pos + count <= N then //test space to shift
begin
mask := mask shl 1; //next bit
Done := true;
result := true;
end
else
if count = K then Done := true
else dec(pos);
end
else dec(pos);
until Done;
for i := count downto 1 do //add removed bits
begin
SH := SH xor mask;
mask := mask shl 1;
end;
end;
In advanceSH zien we deze variabelen:
-
- mask (word): steeds 1 bit set, gebruikt om te vergelijken met bit in SH
- pos (byte): de positie van het "1" bit in mask
- count (byte): het aantal verwijderde "1" bits in SH
Voor de volledigheid nog even wat die doen
| A | B | A and B | A xor B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Met een and operatie selecteren we bits:
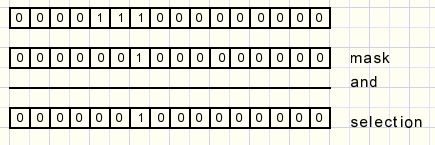
Een xor operatie met "1" draait een bit om ( "0" wordt "1" en "1" wordt "0").
Een xor kan dus een bit setten of resetten.
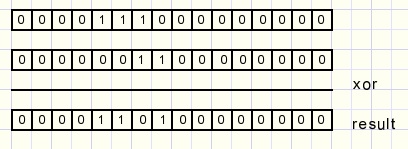
Hieronder staan twee voorbeelden om het algorithe te laten zien.
1.
Beginstand 1000 (keuze 1 uit 4)
De volgende combinatie is dan 0100.
SH=1000 (binair, volgorde bits omgedraaid om van links naar rechts te werken)
-
1. count=0; pos=4; mask=0001(binair)
2. mask=(1 shl pos)
3. (mask and SH)=0--> pos-1
4. mask=0010 (0100,1000)
5. herhaal 2,3,4 tot pos=1
6. (mask and SH)>0-->SH xor mask (drop bit);count+1
7. (pos + count) <= N: Yes--> mask shl 1 (next bit); verlaat repeat loop
8. (count > 0)? Yes-->set mask in SH, herhaal 8.
9. return true, volgende combinatie.
Dat bit wordt op "0" gezet. Variabele count wordt verhoogd om dit aan te geven.
Als pos+count > N dan is er geen plaats om het "1" bit verder te schuiven.
In dat geval zoeken we naar het volgende "1" bit.
Nadat de repeat loop is verlaten worden de verwijderde "1" bits weer ingevoegd.
2.
Beginstand 000000000111 (laatste combinatie van 3 uit 12).
SH=000000000111 (binair)
-
1. count=0;pos=12; (binair)
2. mask=(1 shl pos)
3. (mask and SH)>0-->drop bit; count+1
4. (pos+count)>12 --> pos-1;
5. herhaal 2,3,4 tot count=3--> verlaat repeat loop
6. voeg de 3 verwijderde bits weer in
7. return false, no update

