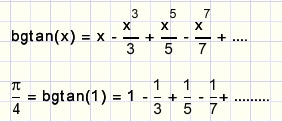 |
Differentiaalrekening (4) |  |
 |
naar deel 1 naar deel 2 naar deel 3Veeltermen
Een veelterm (of polynoom) heeft de gedaante-
y = c0+c1x+c2x2+c3x3+....+cnxn
n heet de graad van de veelterm.
Eerstegraads veeltermen zijn rechte lijnen: y = c0+c1x
Door c0 en c1 te variëren ontstaat steeds een andere lijn.
Tweedegraads polynomen zijn parabolen: y = c0 + c1x + c2x2
In dit artikel wordt differentiaalrekening gebruikt om polynomen te berekenen die
de sinus, cosinus, tangens, logaritmes of machten benaderen.
Die polynomen heten ook wel machtreeksen.
We beginnen met de makkelijkste: y = ex
de afgeleide functies zijn gelijk aan y.
y=y'=y''........
y = ex
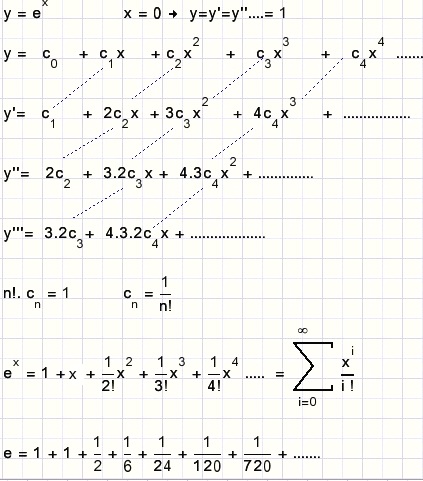
De algemene werkwijze
Een functie wordt benaderd met de machtreeks:-
f(x) = c0+c1x+c2+c1x2+....+cnxn+......
-
f(x) n maal worden gedifferentieerd (= f(n)), dat elimineert de factor x
f(n)(0) worden berekend
x = 0 elimineert de hogere termen.
n!. cn = f(n)(0)
cn = f(n)(0) /n!
ln(x)
Een machtreeks voor ln(x) lukt niet omdat na differentiëren de noemer x wordt enniet gelijk kan zijn aan 0.
Daarom gebruiken we y = ln(1+x)
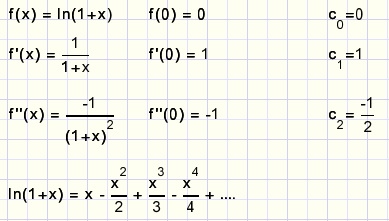
Deze reeks is niet geschikt voor berekeningen omdat er heel veel termen nodig zijn
om een redelijke nauwkeurigheid te bereiken.
Hieronder staat een handiger reeks
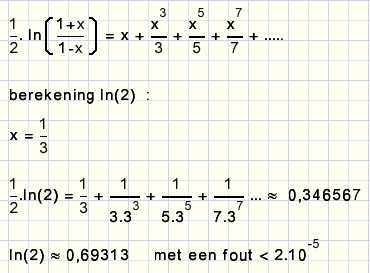
Voorbeeld:
De berekening van 20,7
ln(20,7) = 0,7 . ln(2)-
1. bereken ln(2) = a
2. bereken 0,7 . a = b
3. bereken eb
1. en 3. gebruiken de hiervoor behandelde machtreeksen.
sin(x)
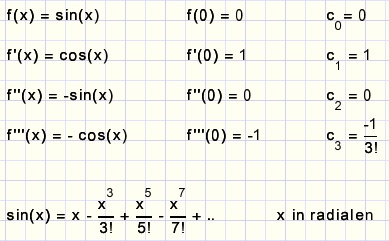
De even termen vallen weg omdat de sinus niet symmetrisch is om de y-as.
cos(x)
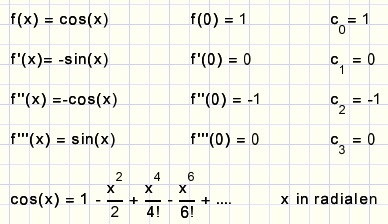
Alleen even termen omdat er symmetrie is t.o.v. de y-as.
tan(x)
tan(x) = sin(x) / cos(x).Het getal π
Tenslotte bepalen we een machtreeks om het getal π te berekenen.Omdat tan(π/4) = 1 is bgtan(1) = π/4.
We zoeken de machtreeks van de functie bgtan(x).
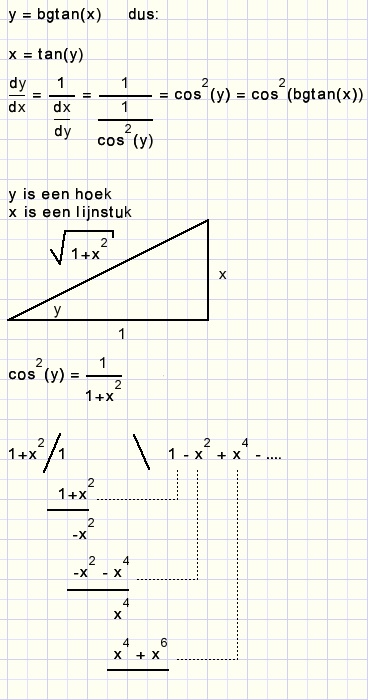
De f'(x) reeks bepalen door te delen bespaart veel werk.
Als y = bgtan(x) dan is dus y'= 1 - x2 + x4 - x6 + ....
Nu even de omgekeerde bewerking van differentiëren om de bgtan(x) functie te vinden:
