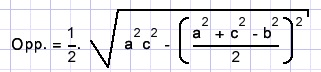de Oppervlakte van een Driehoek

Dit artikel beschrijft de formule van Heron.

Inleiding
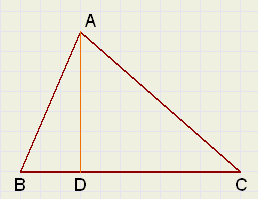
Hiernaast zie je de driehoek ABC.

De oppervlakte daarvan isBC x AD
2


In veel gevallen, zoals bij een stuk land, zijn alleen de lengtes van de zijden bekend.
Een formule voor de oppervlakte van een driehoek waarin alleen de zijden voorkomen is dan handig.

Voor het vinden van die formule is wat algebraïsch gegoochel nodig.
Daarom vooraf een paar trucjes bij het verbouwen van formules.

1.(haakjes wegwerken)
    (p + q)2 = p2 + 2pq + q2
2.(ontbinden in factoren)
    p2 - q2 = (p - q)(p + q)
En als q = v - w dan
    p2 - (v - w)2 = {p - (v - w)}{p + (v - w)} = (p - v + w)(p + v - w)
het gaat erom, de structuur te doorzien.

3.(haakjes wegwerken)
    (p - v + w)(p + v - w) = p2 + pv - pw - pv - v2 + vw + pw + wv - w2
wat te vereenvoudigen is tot
    p2 - v2 + 2vw - w2
en dat is weer gelijk aan
    p2 - (v2 - 2vw + w2) = p2 - (v - w)2
en we zijn op het uitgangspunt terug.

4.(breuken vermenigvuldigen: teller x teller, noemer x noemer)



dus ook (ander voorbeeld):



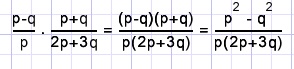
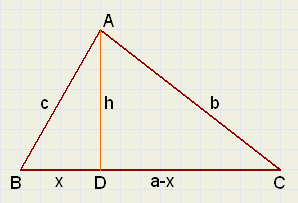
5.(breuken gelijknamig maken en optellen)



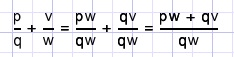
en ook (ander voorbeeld)




Daar gaan we dan
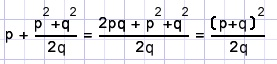
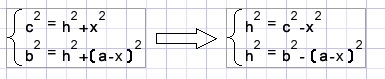
bekijk de driehoek hiernaast:
de basis, tegenover hoek A, heeft lengte a.
BD = x, zodat DC = a - x.
Verder ligt zijde b tegenover hoek B en zijde c
tegenover hoek C.

De aanpak is als volgt:
door toepassing van de stelling van Pythagoras in
driehoeken ABD en ADC zijn twee vergelijkingen op te stellen.



zodat



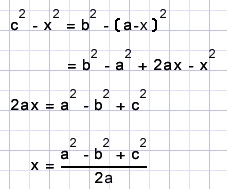
Deze waarde van x, ingevuld in h2 = c2 - x2 = (c - x)(c + x):



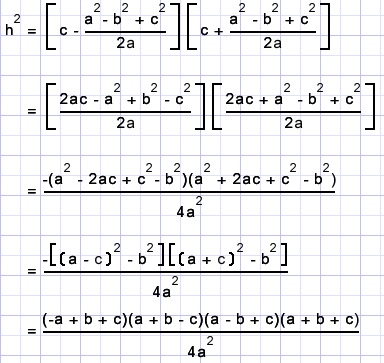
Deze formule is met een trucje nog te vereenvoudigen.
Stellen we de halve omtrek van de driehoek op s, dan is

    ( a + b + c) = 2s
    (-a + b + c) = 2s - 2a
    ( a + b - c) = 2s - 2c
    ( a - b + c) = 2s - 2b
en de formule gaat over in



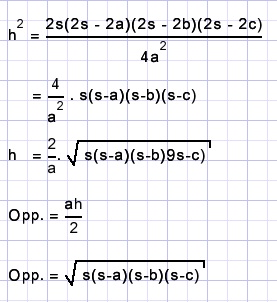
met deze formule is de oppervlakte van een driehoek te berekenen als de zijden bekend zijn.

Dit is de "formule van Heron".

Een voorbeeld
Een driehoek heeft zijden van 7, 8 en 11 meter.
De halve omtrek s = 13.
De oppervlakte



Andere vormen
Zonder de s is de formule:



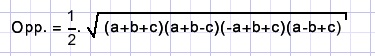
Wat ook is te schrijven als