Beschrijving van het grafieken tekenprogramma

Inleiding

In het vorige artikel beschreef ik hoe functies worden ontleed in basisbewerkingen om de waarde
te kunnen uitrekenen.
Het resultaat is de Director Table, een lijst met rekenkundige bewerkingen gesorteerd van hoge naar lage prioriteit.

Om de functies te tekenen is unit eqdrawer toegevoegd en de code ervan wordt hierna beschreven.
Opmerking:
    - een formule heeft de vorm ...x...y... waarin x en y variabelen zijn en ...... operators
    - een vergelijking heeft de vorm ....x....y = ....x.....y
    - een functie heeft de vorm y = .....x......
Een functie is dus een speciale vorm van een vergelijking.
Functies worden zeer veel gebruikt.
Ze kunnen, omdat ze steeds 1 waarde opleveren, worden gebruikt binnen andere formules.
Een voorbeeld is y = 3sin(x).

In dit project worden 4 soorten functies / vergelijkingen ondersteund.
Het tekenen is opzettelijk simpel gehouden. Het enige doel is het resultaat van de vertaling te tonen.

Het coördinatenstelsel wordt vertegenwoordigd door paintbox1 op form 1, dimensies zijn 640 * 480 pixels.
De oorsprong ligt op pixel positie (320,240).
Het domein van x is -8 ... + 8, het domein van y is -6...+6.
De schaal ligt vast met 40 pixels per cm.

In het algemeen komt tekenen van een grafiek neer op het berekenen van opvolgende (x,y) paren.
Een paar levert een punt van de grafiek en de punten worden met rechte lijntjes verbonden.
Bedenk, dat sommige waarden van x een fout opleveren omdat er bijvoorbeeld de wortel
uit een negatief getal wordt getrokken.
De procedure calculate(var OK : boolean) set OK = false in zo'n geval en het tekenprogramma
moet daar rekening mee houden.

Ondersteunende functies

    function y2pix(y : double) : longInt; //convert y double value naar screen pixel position
    function x2pix(x : double) : longInt; //convert x double naar screen pixel position
    function pix2x(p : longInt) : double; //convert screen pixel x position naar x coordinaat
    function pix2y(p : longInt) : double; //convert screen pixel y position naar y coordinaat
Hieronder behandel ik de teken procedures per type functie.
Kijk op de eqdrawer source code voor verdere details.

Type1 functies {y = ......x........}

Variabele i doorloopt de waarden 0 .. 639.
i wordt omgerekend naar de waarde van x door een call van pix2x(i).
setX(x) geeft x een waarde en calculate(valid) wordt aangeroepen voor de berekening.
y := getY haalt de waarde van de functie op.
Teller vcount houdt het aantal goed berekende punten bij. vcount telt 0,1,2,2,2...
Met waarde 1 vindt een moveto(i, y2pix(y)) plaats, met waarde 2 een lineto(i, y2pix(y)).
Als valid = false, dan wordt vcount = 0 gemaakt.
Ook wordt een test uitgevoerd op het verschil van twee opvolgende y waarden.
Indien te groot, wordt het tekenen onderdrukt om te voorkomen dat asymptoten worden getekend,
zoals in x = 1/x of y = tan(x).
(Dit is een primitieve methode, maar het werkt meestal. Maar beter zou zijn naar de tweede afgeleide te kijken.)

Type2 functies {x = ......y........}

In principe hetzelfde als de type 1 functies, maar x en y zijn verwisseld.

Type3 functies {y = ..v...; x = ....v...}

Nu loopt i van 0 .. 400 en v := 0.025*i.
Deze keuze is gebaseerd op het interval 0..2*pi voor goniometrische functies, dus het tekenen van Lissajous figuren.
Na de call calculate(var OK : boolean) , halen getX en getY de berekende waarden van x en y op.
vcount regelt de keuze tussen de lineto(..,..) en moveto(..,..) methods.

Type4 functies {...y...x... = ...x...y...}

Nu is het tekenproces iets ingewikkelder.
Bedenk, dat een type4 vergelijking de gedaante heeft ....x....y.... = ...x.....y... en zeer ingewikkeld kan zijn.
Probeer bijvoorbeeld (x^2 + y^2)(y^2+x(x+5)) = 20*x*y^2....wat een trifolium oplevert.

Het vertaalproces verandert deze vergelijking in v = (x^2 + y^2)(y^2+x(x+5)) - 20*x*y^2
waarin - prioriteit 2 heeft en = prioriteit 1.
Daarom is na de berekening v gelijk aan 0 als de vergelijking klopte voor x en y.
Het tekenen verloopt als volgt:
v wordt berekend voor elk punt in het coördinatenstelsel (daarom is de methode trager).
Als v = 0 , plot dan het punt.
Als v van teken wisselt (tussen horizontale- of vertikale pixels) , plot dan het punt met de kleinste absolute waarde.
Bedenk, dat in geval van floating point berekeningen antwoorden 0.0000003 of zoiets kunnen zijn in plaats van precies 0.
Ook zijn pixel posities niet altijd mooie gehele waarden.

Variabele i stapt horizontaal van 0 tot 639, j stapt vertikaal van 0 tot 479.
Stel, dat we zojuist alle punten van lijn j hebben berekend.
v is een array[0..639] of double, dat al die berekende waarden van v bevat.
code is een array[0..640] of byte , dat informatie vasthoudt over v[..]:
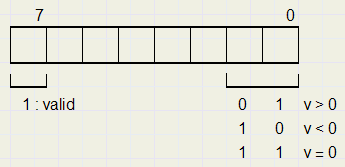
Voor elke nieuwe lijn j+1 wordt v berekend voor elke i. De waarde wordt bewaard in variabele nextV.
De code wordt bewaard in nextcode.
Dan vindt een logische and functie plaats tussen nextcode en code[i].
Bij een uitkomst van $80, zijn beide pixels v[ i ] (op lijn j) en nextV van kolom i op lijn j+1 valid
en treedt tekenwisseling op.
De punt met kleinste absolute value wordt dan geplot.
Hierna wordt v[ i ] := nextV en ook code[ i ] := nextcode.
Als de hele lijn afgewerkt is dan bevat v[ ..] de waarden van v voor lijn j+1 en deze lijn wordt nu getest
op code $83 (0 resultaat) of tekenwisseling.

Vooraf wordt array code[0..640] op 0 gezet.
Zodoende kan tijdens het lezen van lijn 0 geen tekenwisseling gezien worden tussen vertikale pixels.
Door het array 640 lang te maken in plaats van 639, de hoogste kolom, wordt de test voor tekenwisseling
binnen een lijn versimpeld omdat altijd een vergelijking gemaakt kan worden tussen [ i ] en [ i+1 ].

Hiermee besluit ik de beschrijving van de tekenprocedures.