

| Het geitenweitje |  |
Twee boeren bezitten samen een cirkelvormig grasland.
Eén boer wil op de helft ervan een geit laten grazen.
De geit is aangelijnd en de lijn zit met een pen in de grond ergens op de rand van de weide.
De straal van het cirkelvormige weiland is R meter.
Vraag: welke lengte moet de lijn hebben?
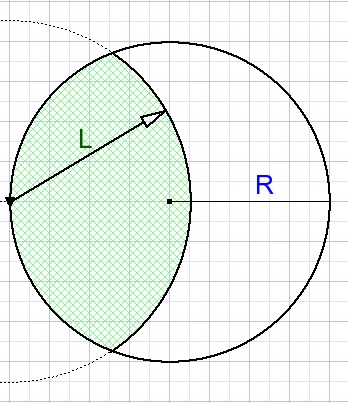
Van de agrarische sector terug naar de schoolbanken zien we twee overlappende cirkels.
Eén met straal L (de grootste, de lijn van de geit) en de ander (het grasland) met straal R.
De afstand van de middelpunten is R.
De oppervlakte A van een cirkel met straal R is A = πR2.
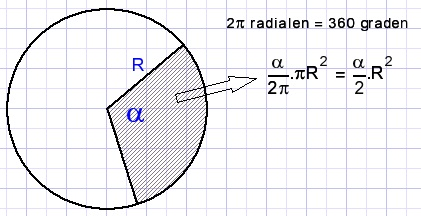
De oppervlakte van een cirkelsegment (taartpunt) met hoek α is (α/2)R2
waarbij de hoek α in radialen is gemeten.
Opmerking:
Bij radialen rekenen we de hoekgrootte in cirkelbogen van een cirkel met straal 1, de omtrek van die cirkel is 2π
Hoe groot is de overlapping?
Dat is niet meteen te zeggen dus we werken in stapjes.
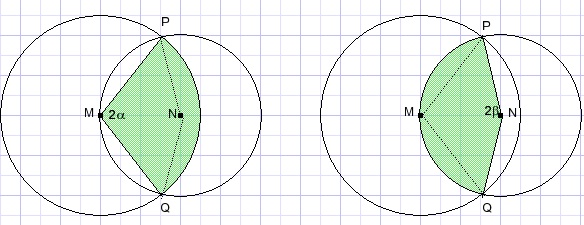
Eerst een segment vanuit de linker cirkel en middelpunt M.
Dan het segment vanuit het middelpunt N van de rechter cirkel.
Tellen we deze oppervlakten op dan is de oppervlakte van vierhoek PMQN dubbel geteld.
Die moet er dus weer van worden afgetrokken.
De oppervlakte van de helft van de rechter cirkel is (π/2)R2 zodat we nu de vergelijking kunnen opstellen:
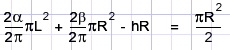
Hierin is hR de oppervlakte van vierhoek PMQN.
R = MN, h is de afstand van P tot MN.
De vergelijking is te vereenvoudigen tot:
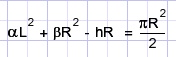
R is een bekend getal.
Bij bekende hoek α zijn β , h en L te berekenen.
Zie onderstaande figuur die ook toont waarom we de hoeken 2α en 2β noemden:
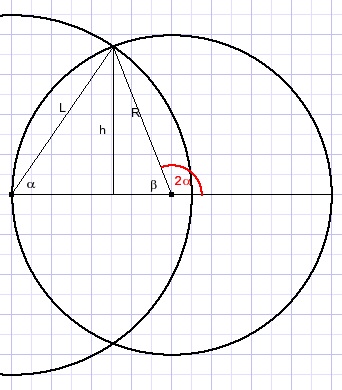
We gaan nu uit van de hoek α en zien dan
-
L = 2Rcos(α)
h = Rsin(β)
β = π - 2α
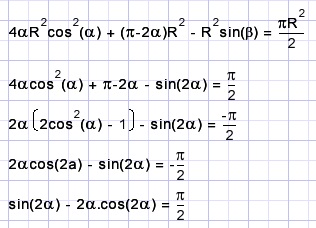
Opmerking:
we pasten de regel toe:
-
2cos2(α)-1 = cos(2α)
-
1. sin2(α) + cos2(α) = 1
2. cos2(α) - sin2(α) = cos(2α)
De volgende stap is α oplossen in de laatste vergelijking van de vorige figuur.
Daar is geen regel voor zoals bijvoorbeeld de ABC formule.
Een methode is inklemming: systematisch proberen en de oplossing steeds dichter benaderen.
Maar sneller is een plotprogramma voor vergelijkingen te gebruiken
en het resultaat in de grafiek af te lezen.
Graphics-Explorer is zo'n functie en vergelijkingen plotter.
Zorg dat radialen zijn ingesteld.
Tik de functies in (kies per functie een verschillende kleur)
-
y = sin(x) - x*cos(x)
y = p/2
en zoom in op het snijpunt.
We lezen af dat x = 1,906,
α = 1,906 * 0,5 = 0,953....radialen
cos(α) = 0,5792
Voor de lengte van geitenlijn L = 2Rcos(α) vinden we dus:
L = 1,158R
De hoek α is in graden: 0,953*180/π = 54,6

