GGD & KGV

download programma om getallen in factoren te ontbinden

Inleiding
Dit artikel gaat over de grondslagen van het rekenen en de wiskunde:
factoren, veelvouden, delers en priemgetallen.
De benodigde voorkennis is basisschool.

de Natuurlijke getallen
Hieronder verstaan we de getallen 0,1,2,3,4,5,.................enzovoorts.
Er zijn oneindig veel natuurlijke getallen.
    natuurlijke getallen = tellen

In dit artikel komen alleen natuurlijke getallen voor en geen breuken,
reële- of complexe-getallen.

Factoren
Een getal waarmee we vermenigvuldigen noemen we een factor.
De vermenigvuldiging 6 * 2 * 4 * 11 bestaat uit 4 factoren:
de eerste factor is de 6, de tweede is de 2 ...enzovoorts.
Een factor geeft dus aan, hoeveel van iets er is.

Dimensie
In de meetkunde denken we bij dimensies aan afmetingen: lengte, breedte, hoogte.
In de natuurkunde wordt met dimensie bedoeld de grootheid, waarin wordt gemeten.
Zo is graden Celsius de dimensie van temperatuur en meter per seconde de dimensie van snelheid.
En de prijs van vlees heeft als dimensie: euro per kilogram.

De eigenschap lengte heeft als dimensie de meter.
Neem eens een paal met een lengte van 2 meter.
Als we die lengte met een factor 3 vermenigvuldigen, dan ontstaat een paal van 6 meter lang.
De eigenschap lengte van de paal is veranderd, maar het is nog steeds een paal,
niets meer en niets minder.

Een factor heeft geen dimensie.
Als we een grootheid (gewicht, tijd, afstand) met een factor vermenigvuldigen,
dan verandert het aantal of een eigenschap, maar de dimensie blijft hetzelfde.

Als we getallen vermenigvuldigen die alletwee een dimensie hebben, dan ontstaat iets nieuws.
Zo is meter * meter = vierkante meter en bij elektriciteit: stroom * spanning = vermogen.

De hoeveelheid werk die nodig is om een computerspel te maken, kunnen we uitdrukken in
het product van mannen en jaren. Dan ontstaat een grootheid met dimensie manjaren.
(lees "mens" voor "man").

In dit artikel werken we met dimensieloze getallen.
We nemen aan, dat alle getallen factoren zijn.

Termen
Getallen, die worden opgeteld (of afgetrokken), noemen we termen.
12 + 9 + 23 is een optelling van 3 termen.
Alleen termen met gelijke dimensie kunnen worden opgeteld.
Als a en b onbekende dingen zijn, dan is de optelling a + b niet mogelijk.
Als a een factor 3 is en b een factor 5 en het betrekking heeft op het aantal
kippen, dan geldt: a + b = 3 + 5 = 8 {kippen}.

Veelvouden
met de veelvouden van 5 wordt bedoeld de rij natuurlijke getallen:
    5, 10, 15, 20, 25,...........
Algemeen:
    de veelvouden van 5 hebben de vorm 5*k , waarbij k = 1,2,3,4,5,6,........

    veelvouden van 5
Voorbeeld:
de veelvouden van 11 zijn: 11, 22, 33, 44, 55, 66, 77, .......

Als we een berg stenen hebben en het aantal is een veelvoud van 5, dan kunnen die
stenen op stapeltjes van 5 worden gelegd, waarbij geen steen overblijft.

Delers
Als stenen op stapeltjes van 5 liggen en we tellen het aantal stapeltjes,
dan komt dat neer op delen door 5.
Anders: als 5 personen de stenen eerlijk verdelen, dan krijgt elk een steen
van elk stapeltje.
Zo'n eerlijke verdeling, waarbij geen steen overblijft, is alleen mogelijk als
het totale aantal stenen een veelvoud was van 5 of :
geschreven kan worden in de de vorm 5.k.

De volgende uitspraken komen dus op hetzelfde neer:
(als er één klopt, dan kloppen de andere ook)
    - 35 is deelbaar door 5
    - 35 is een veelvoud van 5
    - 35 bevat een factor 5
    - de rest bij deling van 35 door 5 is nul
    - 35 kan geschreven worden in de vorm 5.k

Priemgetallen
Dat zijn de (natuurlijke) getallen, die niet in factoren ontbonden kunnen worden of,
anders gezegd: getallen, die alleen door zichzelf en door 1 deelbaar zijn.

De eerste tien priemgetallen zijn 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Elk natuurlijk getal is een priemgetal of kan op unieke manier
worden geschreven als product van priemgetallen.

Ontbinden in priemfactoren
beschouw eens:
    100 = 2 * 50
    50 = 2 * 25
    25 = 5 * 5
zodat:
    100 = 2 * 2 * 5 * 5 = 22 * 52
100 schrijven als 22 * 52 noemen we: ontbinden in priemfactoren.
Priemgetallen zijn de bouwstenen van de natuurlijke getallen.

Elk getal kan maar op één manier in priemfactoren worden ontbonden.
Getallen zijn dus gelijk, als ze dezelfde priemfactoren bevatten.

Bij 52 noemen we 5 het grondtal en 2 de exponent.
De exponent geeft aan hoeveel factoren van het grondtal er zijn.

De getallen 2 en 5 kunnen niet in kleinere factoren worden ontbonden:
een aantal van 2 of van 5 stenen kan alleen op één rijtje of op één stapeltje worden gelegd.

de zeef van Eratosthenes
Eratosthenes was een Grieks wiskundige, die leefde van 276 - 194 v. Chr.

Zijn "zeef" is een methode om priemgetallen op te sporen.
Om alle priemgetallen tot bijvoorbeeld 100 te vinden, schrijven we de natuurlijke getallen van
2 tot 100 in een tabel.
Ga nu als volgt te werk:
    1. Markeer het eerste priemgetal, dat is de 2.
    2. Streep alle veelvouden van dit priemgetal (4,6,8...) door, veelvouden zijn geen priemgetal.
    3. Ga naar het volgende niet doorgestreepte getal, dat is de 3, het volgende priemgetal.
    4. Streep alle veelvouden (6,9,12,15,...) door.
    5. Ga naar het volgende (niet doorgestreepte) priemgetal.
    6. Streep alle veelvouden van dit priemgetal door.
    7. Herhaal stappen 5. en 6.
Hieronder zie je een tabel, waarin de "zeef" is toegepast.
Elk veelvoud van een priemgetal heeft een aparte kleur gekregen.
                   2   3   4   5   6   7   8   9
          10  11  12  13  14  15  16  17  18  19
          20  21  22  23  24  25  26  27  28  29 
          30  31  32  33  34  35  36  37  38  39
          40  41  42  43  44  45  46  47  48  49
          50  51  52  53  54  55  56  57  58  59
          60  61  62  63  64  65  66  67  68  69
          70  71  72  73  74  75  76  77  78  79
          80  81  82  83  84  85  86  87  88  89
          90  91  92  93  94  95  96  97  98  99
In de tabel hierboven zijn de veelvouden van 2 paars gekleurd.
Het eerste paarse getal is 4.
De veelvouden van 3 zijn groen-blauwgekleurd.
Het eerste getal van deze kleur is 9.
Hieruit is een belangrijke conclusie te trekken:
als de veelvouden van priemgetal p zijn gemarkeerd, dan weten we zeker,
dat alle niet gemarkeerde getallen in de tabel die kleiner zijn dan p2
priemgetallen zijn.
Om alle priemgetallen tot 1000 te vinden, hoeven alleen de veelvouden van de
priemgetallen tot en met 31 te worden doorgestreept.

Systematisch ontbinden in factoren
Als voorbeeld ontbinden we 4126200 in factoren.

Een eenvoudige, maar omslachtige methode
    - sla 4126200 op in het geheugen van je rekenmachine
    - deel door 2, het eerste priemgetal, de uitkomst is 2063100
    - bewaar de factor 2 en sla 2063100 op
    - deel opnieuw door 2, uitkomst is 1031552
    - bewaar factor 2, sla 1031552 op
    - deel weer door 2, uitkomst is 515775
    - bewaar de 2, sla 515775 op
    - deel weer door 2, uitkomst is 257887,5 (getal bevatte dus geen factor 2)
    - reload 515775
    - deel door 3, uitkomst is 171925
    - bewaar factor 3, sla uitkomst op
    - deel opnieuw door 3, uitkomst is 57308,33333 (geen factor 3 meer aanwezig)
    - reload 171925
    - deel 171925 door 4
    (dit zal geen factor opleveren, omdat 4 = 2 * 2, de factoren 2 zijn al weg)
    - deel 171925 door 5, antwoord is 34385
    - sla antwoord op, bewaar de 5
    - deel opnieuw door 5, antwoord is 6877
    - sla antwoord op, bewaar de 5
    - deel weer door 5, antwoord is 1375,4
    - reload 6877
    - deel door 6,7,8,9,10,11,12....totdat deling uitkomt, reload als deling niet uitkomt.
    - 6877 : 13 = 529, sla antwoord op, bewaar factor 13.
    - deel 529 door 13,14,15,16,17,18,19,20,21,22.....reload steeds, omdat deling niet uitkomt
    - 529 : 23 = 23, bewaar factor 23, sla 23 op.
    - 23 : 23 = 1, bewaar factor 23.(laatste factor niet vergeten)
De bewaarde factoren zijn: 2,2,2,3,5,5,13,23,23, zodat:
    4126200 = 23*3*52*13*232
Eerste verbetering.
 Elk priemgetal boven de 3 heeft de vorm 6.k - 1 of 6.k + 1.
Immers, 6.k, 6.k + 2, 6.k + 3, 6.k + 4 kunnen geen priemgetal zijn, want ze zijn
deelbaar door 6, 2, 3 of 2.
We kunnen ons dus beperken tot de delers 2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37,.....

Tweede verbetering.
 Nog beter is het, de eerste priemgetallen in een tabel beschikbaar te hebben en de
delers uit deze tabel te halen.

Derde verbetering.
 Stel, dat we 5113 in factoren willen ontbinden.
Alle priemgetallen worden als deler geprobeerd.
Op een bepaald moment delen we 5113 : 71 = 72,01....
dan delen we 5113 : 73 = 70,04...
Voor het eerst is de uitkomst kleiner dan de deler.
Nu kunnen we stoppen, want als 5113 een factor bevatte, dan hadden we die
al eerder gevonden. 5113 is dus een priemgetal.

Handige notatie:
    quotientdeler
    41262002
    20631002
    10315502
    5157753
    1719255
    343855
    687713
    52923
    23
De delers, samen met het laatste quotient, vormen de factoren.

het KGV (kleinste gemeenschappelijke veelvoud)
De veelvouden van 12 zijn: 12, 24, 36, 48, 60, 72, 84, 96, .....
De veelvouden van 15 zijn: 15, 30, 45, 60, 75, 90, 105, 120, ......
Het kleinste gemeenschappelijke veelvoud is dus: 60.

Want:
    60 = 5 * 12
    60 = 4 * 15
Notatie:
    KGV(12,15) = 60
12 is een deler van 60, want 60 bevat alle factoren, die 12 ook bevat.
15 is een deler van 60, want 60 bevat alle factoren, die 15 ook bevat.

Factoren die zowel in 12 als in 15 zitten (de 3) hoeven niet dubbel geteld te worden.

    KGV(6,10) = 30
Berekening KGV(12,15) door ontbinden in factoren:
    12 = 22 * 3
    15 = 3 * 5
Beschouw nu de rijtjes factoren en neem steeds het grootste aantal, dat bij elke ontbinding
is gevonden.
Dat zijn 2 factoren 2, bij de 12, 1 factor 3 en 1 factor 5 bij de 15.
Dus KGV(12,15) = 22 * 3 * 5 = 60.

Voorbeeld:
    2520 = 23 * 32 * 5 * 7
    29700 = 22 * 33 * 52 * 11
Zodat:
    KGV(2520,29700) = 23 * 33 * 52 * 7 * 11 = 415800

de GGD (grootste gemeenschappelijke deler)
De delers van 120 zijn:
    2,3,4,5,6,8,10,12,15,20,24,30,40,60,120
De delers van 48 zijn:
    2,3,4,6,8,12,16,24,48
De grootste gemeenschappelijke deler is 24.

Alle factoren van 24 zitten zowel in 120 als in 48.
24 is opgebouwd uit alle gemeenschappelijke factoren van 120 en 48.

Notatie:
    GGD(120,48) = 24
Berekening GGD(120,48) door ontbinden in factoren:
    120= 23 * 3 * 5
    48 = 24 * 3
Beschouw nu de rijtjes factoren en neem steeds het kleinste aantal, dat in elke
ontbinding is gevonden.
Dus 3 factoren 2, 1 factor 3 en 0 (geen) factor 5, zodat:
    GGD(120,48) = 23 * 3 = 24
Voorbeeld:
    2520 = 23 * 32 * 5 * 7
    29700 = 22 * 33 * 52 * 11
Zodat:
    GGD(2520,29700) = 22 * 32 * 5 = 180

Het verband tussen GGD en KGV
Bij de berekening van het KGV kozen we per factor de grootste exponent.
Bij de berekening van de GGD kozen we juist per factor de kleinste exponent.
Kiezen we zowel de grootste als de kleinste exponent dan ontstaat simpelweg
het product van de twee getallen, zodat:
    KGV(a,b) * GGD(a,b) = a * b
Dit is een handige rekenregel.

Voorbeeld:
    GGD(2520,29700) * KGV(2520,29700) = 415800 * 180 = 74844000
    maar ook: 2520 * 29700 = 74844000

Relatieve priemgetallen
Getallen heten "relatief priem" als ze geen gemeenschappelijk factoren bevatten.
Zoals bijvoorbeeld: 16 en 25.
Voor relatieve priemgetallen a en b geldt: GGD(a,b) = 1.

Het theorema van Euclides
Euclides was een Griekse wiskundige, die leefde van ongeveer 325 - 265 v.Chr.
Hij bedacht een handige manier om de GGD van twee getallen te berekenen,
zonder in factoren te hoeven ontbinden.

Hier komt het op neer: (als a > b)
    GGD(a,b) = GGD(a-b,b)
Door deze regel herhaald toe te passen wordt de GGD uit steeds kleinere getallen
berekend.

Voorbeeld:
    GGD(630,300) = GGD(330,300) = GGD(300,30) = .... = GGD(30,30) = 30.
Bewijs: GGD(a,b) = GGD(a - b, b)
Het bewijs bestaat uit 2 delen:
    1. als d een factor is van a en b, dan is d ook een factor van a - b
    {er raakt niets weg}
    2. als d een factor is van a - b en van b, dan is d ook een factor van a, dus van a en van b
    {er komt niets bij}
    - =
    verschil veelvouden van 5 heeft ook factor 5

bewijs 1.
    neem aan:
    a = p.d en b = q.d, waarbij p en q relatief priem.
    Dan is:
    a - b = p.d - q.d = d(p - q)
    en
    (a - b)/d = p - q is een geheel getal.
    Dus (a - b) heeft een factor d.

Bewijs 2.
    neem aan:
    a - b = d.p en b = d.q
    Dan is:
    a = d.p + b = d.p + d.q = d(p + q)
    oftewel:
    a heeft een factor d.
    b heeft ook een factor d.
    zodat:
    a en b een factor d gemeenschappelijk hebben
    Conclusie: een gemeenschappelijke factor van a - b en b is ook een gemeenschappelijke factor van a en b.
    Er komt geen factor bij.

Voorbeeld:
Herhaalde toepassing van het theorema van Euclides,
berekening van GGD(110901,35553):
    110901 = 3 * 35553+4242
    35553 = 8 * 4242+1617
    4242 = 2 * 1617+1008
    1617 = 1 * 1008+609
    1008 = 1 * 609+399
    609 = 1 * 399+210
    399 = 1 * 210+189
    210 = 1 * 189+21
    189 = 9 * 21+0
zodat:
    GGD(110901,35553) = 21

Toepassingen
KGV
1.breuken gelijknamig maken.
1
85
 + 
1
119
 = 
1
5 · 17
 + 
1
7 · 17
 = 
7
5 · 7 · 17
 + 
5
5 · 7 · 17
 = 
12
595

2.samenvallen van periodieke verschijnselen.
Twee autobussen, A en B vertrekken gelijk van een busstation.
A rijdt heen en weer 70 minuten, B doet 50 minuten over een ronde.
Over KGV(70,50) = 350 minuten treffen ze elkaar weer bij het busstation.

 GGD
1.factoren buiten haakjes halen.(kleinste pakketten samenstellen)
2475 a + 1950 b = 3 2 · 5 2 · 11 a + 2 · 3 · 5 2 · 13 b = 3 · 5 2 (3 · 11 a + 2 · 13 b) = 75 (33 a + 26 b)

2.vereenvoudigen van breuken.
1950
2475
 = 
2 · 3 · 5 2 · 13
3 2 · 5 2 · 11
 = 
26
33

Vragen
a. wat zijn de eerste 10 veelvouden van 23?

ontbind in factoren:

b. 12
c. 150
d. 375
e. 147

bereken:

f. KGV(150,375)
g. KGV(147,375)
h. GGD(150,375)
i. GGD(147,375)

Een verpakkingsbedrijf moet uit 34650 potten jam en 36300 blikjes vis
zoveel mogelijk gelijke pakketten samenstellen.

j.hoeveel pakketten worden dat en wat is de inhoud van een pakket?

Drie tandwielen van 24, 30 en 40 tanden zijn gekoppeld met elkaar.
Elk tandwiel is voorzien van een pijltje.

k.hoeveel tanden moeten de tandwielen opschuiven om weer in de oorspronkelijke
stand te staan?

Een rechthoekige tegel heeft afmetingen 56 * 98.
Met deze tegels wordt een vierkante oppervlakte bestraat.

l. hoe groot is de zijde van het kleinst mogelijke vierkant?

m. hoe groot is de zijde als de tegel afmetingen a * b heeft?

n. ga na of 5419 een priemgetal is.

o. ga na of 4587 een priemgetal is.

p. ga na of 62809 een priemgetal is.

Zie tekening:
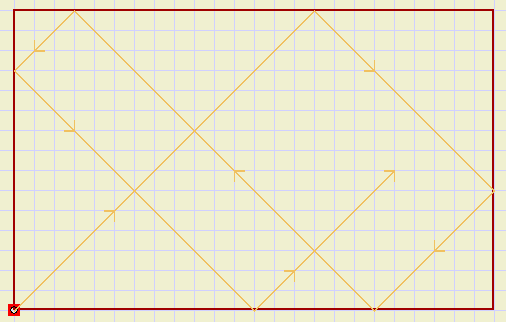    spiegelende kamer met lichtbron
Een lichtstraal beweegt door een rechthoekige kamer met spiegelende wanden.

q. hoeveel hokjes moet de straal doorlopen om weer bij de lichtbron
uit te komen?(kamer 24 * 15 hokjes)

r. hoeveel hokjes, als de kamer zijden van a * b hokjes heeft?

Voor wie al wat meer wiskunde kent:
Iemand moet een tabel berekenen met de vierkantswortels van 1 t/m 1000.
De nauwkeurigheid is drie decimalen, dus alle wortels berekenen is veel werk.
Bedenkend, dat
\a b
 = 
\a
 
\b
is veel werk te besparen.

s. leg uit hoe.

Een rechthoek van 585 * 825 cm2 moet worden verdeeld in gelijke vierkanten.
(werk alleen op hele cm.)

t. hoe groot is de zijde van het grootst mogelijke vierkant?

u. hoeveel van die vierkanten zijn er?



Antwoorden:
----------------
a. 23 46 69 92 115 138 161 184 207 230
b. 22.3
c. 2.3.52
d. 3.53
e. 3.72
f. 750
g. 18375
h. 75
i. 3
j. 1650 * ( 21 jam + 22 vis)
k. 120
l. 392
m. KGV(a,b)
n. ja
o. nee
p. nee, 107 * 587
q. 240
r. KGV(2a,2b)
s. alleen wortels uit priemgetallen berekenen
t. 15
u. 2145
-------------------