Hangende kabels

Probleem

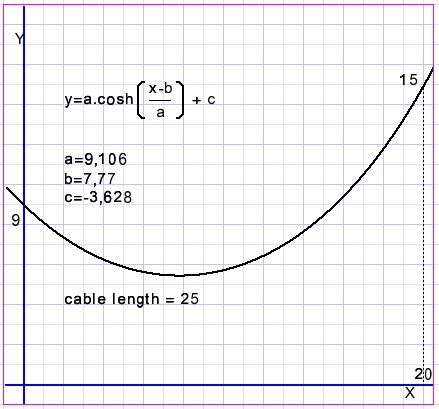
Een niet rekbare maar flexibele kabel is aan twee punten bevestigd.
Welke functie beschrijft deze curve?
In dit artikel leg ik dat uit.

Gegeven is de lengte L van de kabel en de coördinaten van de ophangpunten: (x1,y1) en (x2,y2)

Basiskennis

Voor een bewijs van de twee functies hierna verwijs ik naar Wikipedia,
zoek met termen "catenary" of "hanging cables".
De algemene formule die een hangende kabel beschrijft is:
    y = a.cosh(x/a).....................waarbij cosh(x) = (ex+e-x)/2
De booglengte L1 tussen punten x=0 en x = x1 is:
    L1=a.sinh(x1/a).....................waarbij sinh(x)=(ex-e-x)/2
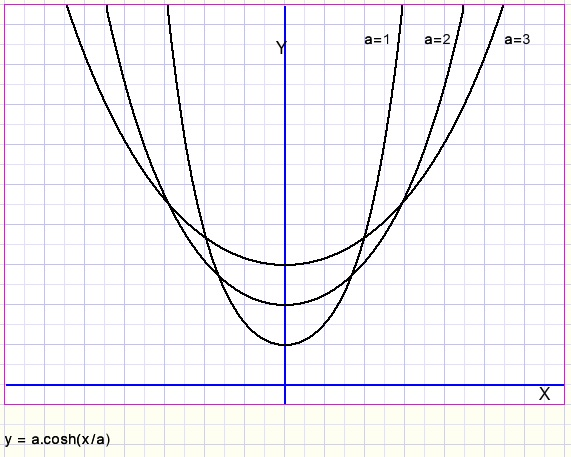
Het plaatje hieronder laat een paar gevallen zien voor verschillende waarden van a:



Het minimum ligt op de y-as die ook symmetrielijn is.
A is de schaalfactor, zowel horizontaal als vertikaal.

Om te beginnen is dit ons probleem:



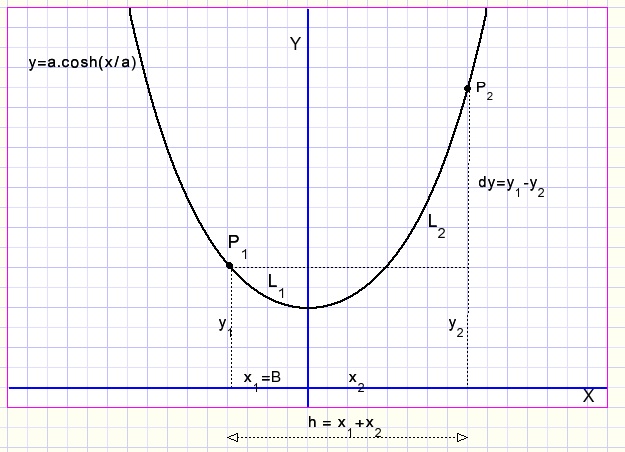
Bekend zijn de coördinaten van punten P1 en P2 dus ook h = x1+x2
In de grafiek ligt het minimum a boven de x-as.

Ons uitgangspunt zijn de kabellengte L=L1+L2,
het vertikale verschil dy = y2-y1 en de horizontale afstand h=x1+x2.

Dit is wat we weten:



Eerst gaan we op zoek naar a.
Daarvoor moeten we x1, x2, y1, y2 vervangen door de bekende waarden L, h en dy.

De berekening van a




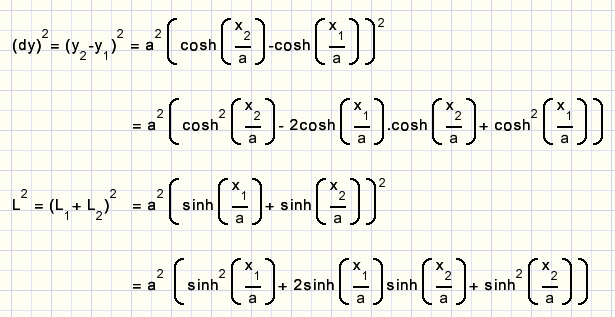
Pas deze regel toe:



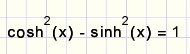
en dan:



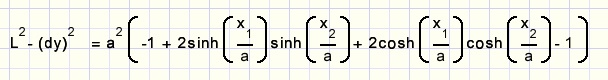
Pas deze regel toe:



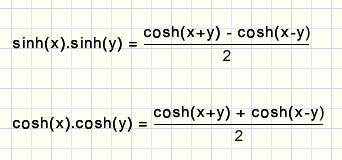
en dan:



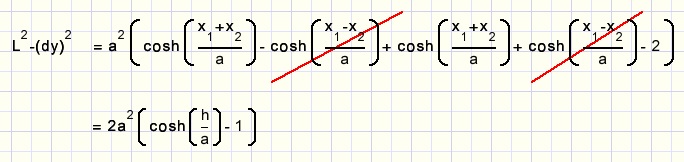
Nog één extra stapje door toepaasing van deze regel:



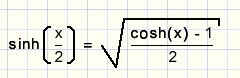
en a is gevonden:



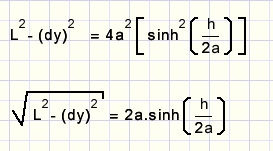
In deze vergelijking moet a numeriek worden opgelost.(uitleg verderop)

De berekening van b=x1

Met a bekend kan b=x1 worden berekend.

Toegepaste regel:



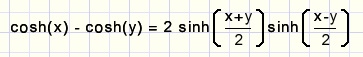
en dan:



In de uiteindelijke formule willen we P1 op de Y-as hebben, dus een horizontale verschuiving met b = x1 is nodig.
Opmerking: vervang x door (x-b) om de grafiek b naar rechts te schuiven.
Na deze verschuiving is x1 = 0, x2 = h.
Tot nu toe hebben we alleen dy gebruikt, niet y1 en y2.
Het minimum van de curve ligt altijd a boven de X-as.

Om te zorgen dat de punten P1 en P2 op de kabel liggen is een vertikale verschuiving nodig.
De gezochte formule is:



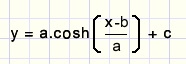
De berekening van c


Met bekende a,b en y1 is c direct te bepalen:



Delphi programma

In dit programma is de horizontale afstand h altijd 20. 
procedure calculateArc(var A,B,C : double; y1,y2: double);
//given: linelength, (0,y1) , (20,y2)
//calculate formula y = A*cosh((x-B)/A) + C
var a1,a2,QLV,V,dy : double;
begin
 a1 := 1;
 a2 := 100;
 dy := y1-y2;
 QLV := 0.5*sqrt(sqr(linelength)-sqr(dy));
 repeat
  A := 0.5*(a1+a2);
  V := A*sinh(10/A);
  if V > QLV then a1 := A;
  if V < QLV then a2 := A;
 until abs(QLV - V) < 0.0001;
 B := A*arcsinh(dy/(2*A*sinh(10/A))) + 10;
 C := y1 - A*cosh(B/A);
end;
a wordt numeriek opgelost door inklemming tussen a1 en a2.
Opmerking: by de uses clausule mag "math" niet ontbreken.

Tot besluit nog een plaatje: