Lineaire Regressie

Inleiding
In dit artikel wordt een handige formule afgeleid voor de regressielijn door een puntenwolk.

Gegeven zijn een aantal punten (x_i, y_i)...waarbij i = 1,2,...,n
Gevraagd wordt de lijn y = ax + b waarvoor de afwijking met deze punten minimaal is.

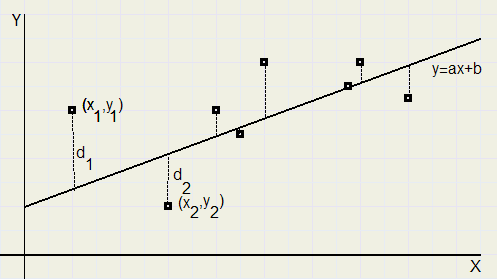
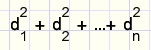
Een veelgebruikte maat voor de afwijking is de som van de kwadraten van de verschillen:

in het geval van n punten.

Nu geldt voor punt i:

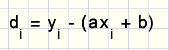
Voordat we verder gaan, eerst wat notatie en rekenregels invoeren.

Definitie

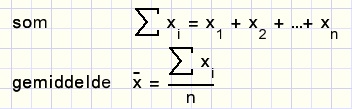
Rekenregels

Als c een constante is:

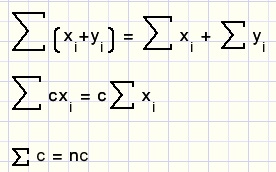
toepassing:

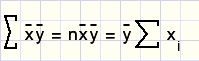
De formules voor a en b van regressielijn y = ax + b
De functie f(a,b) van de som van de kwadratische afwijkingen van punten 1..n is:

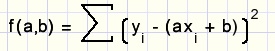
f(a,b) differentiëren we eerst naar a, waarbij b constant wordt gehouden en daarna naar b,
waarbij a constant wordt gehouden.
differentiëren naar a:

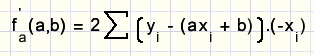
differentiëren naar b:

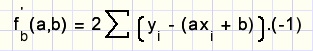
Voor de beste benadering, dus kleinste kwadratische afwijking, moeten beide afgeleiden = 0 zijn.
Dat levert op het stelsel vergelijkingen:

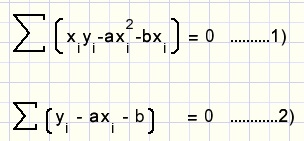
Uit ....2) volgt:

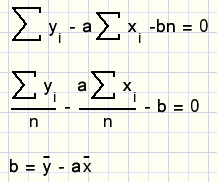
Dit resultaat voor b vullen we in bij ........1)

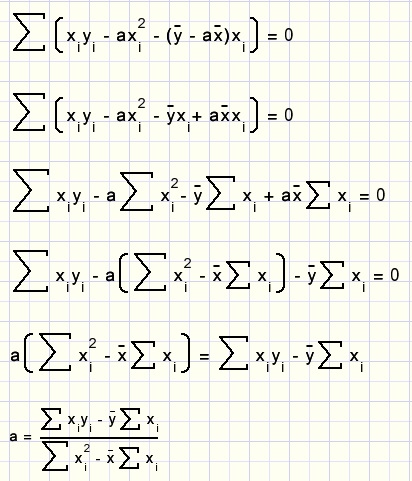
In principe zijn nu formules voor a en b gevonden.
De bovenstaande waarde van a kan immers bij .......3) worden ingevuld om b te berekenen.
Met wat gegoochel kan de formule voor a echter in een eleganter vorm worden gegoten.
We pakken teller en noemer afzonderlijk aan.

1. de teller

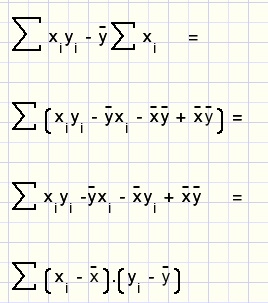
2. de noemer

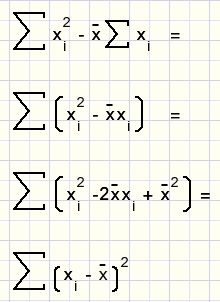
samengevat:

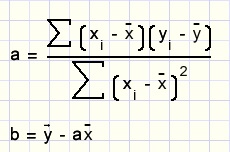
Opmerking:
Kijk [hier] voor een artikel over de beste benadering van een puntenwolk door een n-de graads kromme.
Het is een mooie toepassing van de lineaire algebra.