logigrammen oplossen

De opgave

5 personen: Mary, Wim, Peter, Anne en Corry,
5 opdrachten: huiswerk, examen, proefwerk, tentamen en overhoring
5 vakken: taal, rekenen, aardrijkskunde, geschiedenis en biologie
5 cijfers: 3,5,6,7 en 9

De voorwaarden zijn:
1) De persoon die het tentamen maakte, kreeg een hoger cijfer
   dan degene die moest rekenen, maar een lager cijfer dan Corry.
2) Peter is niet degene die huiswerk moest maken. Hij heeft echter
   een hoger cijfer dan Anne, maar een lager cijfer dan degene die
   geschiedenis deed. We weten ook dat Peter geen 4 en ook geen 6 punten
   meer kreeg dan de persoon die examen deed.
3) De leerlinge die het proefwerk maakte, kreeg een hoger cijfer
   dan Mary die geen taal deed, maar een lager cijfer dan degene
   die biologie deed.
4) Wim deed aardrijkskunde en kreeg een hoger cijfer dan degene
   die taal deed. Hij kreeg echter een lager cijfer dan de persoon
   die een overhoring had.
----------------------------------------------------------------------------
Welke opdracht, vak, cijfer hoort bij wie?

Toelichting bij het programma

--------------------------------
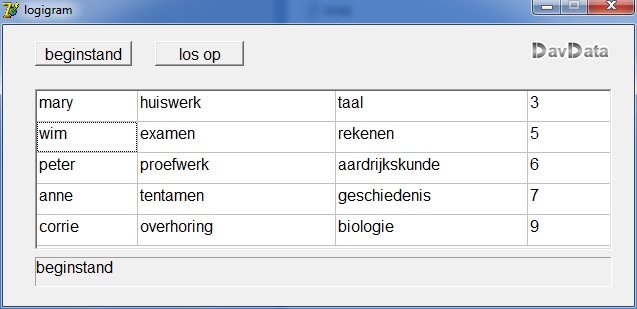
Uitgangspunt is deze tabel:

--------------------------------------------------------------
                             kolom                            |
--------------------------------------------------------------
    0           1             2                3              |
persoon |   opdracht  |      vak        |   cijfer  |     rij |
--------------------------------------------------------------
mary      huiswerk       taal                 3     |      0  |
wim       examen         rekenen              5     |      1  |
peter     proefwerk      aardrijkskunde       6     |      2  |
anne      tentamen       geschiedenis         7     |      3  |
corrie    overhoring     biologie             9     |      4  |
--------------------------------------------------------------

Bij het zoekem maar oplossingen blijven de personen in kolom 0
op hun plaats staan.
De rijen in kolommen 1 t/m 3 verwisselen echter, tot een combinatie
is gevonden zonder conflicten.

De opdrachten, vakken, personen en cijfers worden in het programma
aangeduid met hun rij in de tabel hierboven, dus als 0,1,2,3 of 4.
Omdat de personen niet van plaats wisselen, vormen die tevens het
nummer van een rij.

Per kolom zijn er 5! = 120 volgorden van de opdrachten,vakken of cijfers.
Een volgorde wordt met een getal van 0..119 aangegeven.
Er zijn dus 3 van die getallen nodig, ze staan in array permNr[1..3].
(permNr staat voor permutatie nummer)
PermNr[2] geeft de permutatie aan van kolom 2.

In de tabel hierboven is van elke kolom permutatie 0 weergegeven.

De getallen permutNr[1], permutNr[2] en permutNr[3] vormen een telwerk.
Elke teller telt van 0..119, bij 120 gaat de teller over de kop naar 0
en verhoogt de volgende teller.
PermutNr[1] van 120 naar 0 verhoogt PermuNr[2], enzovoort.
Zo worden alle tellerstanden systematisch doorlopen.

Bij elke stand 0..119 hoort een volgorde van de elementen
in een kolom.

De omzetting van tellerstand naar permutatie (volgorde) gaat zo:
(stel dat we permutatie nummer 88 willen berekenen)

   maak eerst permutatie 0 , dat is 0 1 2 3 4
   deel 88 door 24 = 3  (88 div 24 = 3)    opm. 24 = 4!
   pak het 3e element uit de rij, dat is de -3-
   de rest bij deling van 88 door 24 = 16   (88 mod 24 = 16)
   haal de 3 weg uit de rij, dat levert de nieuwe rij 0 1 2 4 x
   deel 16 door  6 , 16 div 6 = 2
   neem het 2e element uit de rij, dat is de -2-
   16 mod 6 = 4   opm. 6 = 3!
   haal de 2 weg uit de rij, dat levert 0 1 4 x x
   4 div 2 = 2
   neem 2e getal uit de rij, dat is de -4-
   4 mod 2 = 0
   haal de 4 weg uit de rij, dat levert 0 1 x x x
   0 div 1 = 0
   neem 0e getal uit de rij, dat is de -0-
   de nieuwe rij wordt 1 x x x x
   pak nu het overgebleven getal, de -1-
   De volgorde nummer 88 is dus 3 2 4 0 1

Wordt deze volgorde toegepast op de kolom "opdracht" dan wordt die kolom:

   tentamen
   examen
   overhoring
   huiswerk
   examen

Maar de volgorde kan natuurlijk ook op andere kolommen slaan.

Dat achtereenvolgens wordt gedeeld door 24, 6, 3 en 1 zit zo:
er zijn 24 permutaties van 4 elementen. Deze kunnen als modulo 24
teller worden beschouwd.
Bij de eerste 24 permutaties zal de -0- voorop staan.
Bij permutaties 24..47 zal de 1 voorop staan. Enzovoort.

getal div 24 bepaalt dus het meest linkse element.
We verwijderen dit cijfer uit de rij 0 1 2 3 4, want het mag niet
opnieuw worden gekozen.
getal mod 24 is de rest bij deling en met dit getal gaan we verder.
Er zijn nu nog 4 cijfers te bepalen.
De laagste 3 vormen een modulo 3! = 6 teller zodat het hoogste cijfer
wordt bepaald door rest div 6.
En rest = rest mod 6 is wat overblijft.
Elk gevonden getal verwijderen we uit de rij.
Tenslotte wordt het laatste, overgebleven, getal aan de volgorde toegevoegd.

Om niet steeds dezelfde permutaties te hoeven berekenen wordt de tabel
permuts[0..4,0..119] bij het starten van het programma gevuld.

Succes!