download
program		 Solving Ax + By = C
Introduction
This article describes how my program "Euclid" solves x,y in the equation Ax + By = C, for integers A,B,C,x,y.

These type of equations arise from puzzles like this:

    A collector of ancient cars leaves his 4 children the following will:

    John: 40% of the cars is for you. Of the remaining 60%, grant 5 of your choice to a museum.
    Helen: 40% of the remaining cars is for you. After your choice, grant 3 of the remaining cars to a museum.
    Emily: 40% of the remaining cars is for you. After your choice, grant 1 car to a museum.
    Roderick : the remaining cars are yours.
Question: how many cars should this collection count minimally, to make such a distribution possible?

Say, the collection counts x vehicles, then:
    0.6(0.6(0.6x - 5) - 3) - 1 should be a positive integer.
If Roderick receives y cars, then:
    0.216x - 4.6 = y
    216x - 1000y = 4600
So, positive integers x and y must be found, that satisfy the above equation.

The core of solving such equations is the use of the Euclidean Algorithm.
So, first this algorithm is discussed.
After that, we will see how the algorithm is applied to obtain the desired results.

The Euclidean Algorithm
A somewhat free interpretation of the Euclidean algorithm is:
    gcd(A,B) = gcd(A - B,B) where gcd means "greatest common divisor"
In words:
    instead of calculating gcd(56,35), we may calculate gcd(21,35)
gcd(56,35) = gcd(21,35) = gcd(35,21) = gcd(14,21) = gcd(21,14) = gcd(7,14) =
gcd(14,7) = gcd(7,7) = 7.

A proof can be constructed of 2 sub-proofs:
    1. if d is a factor of A and B, then d is a factor of A - B
    {no common factor is lost}
    2. if d is a factor of only A or B, then d cannot be a factor of A - B
    {no new common factor is introduced}
proof 1.
    assume:
    A = ad and B = bd then:
    A - B = ad - bd = d(a - b)
    and
    (A - B)/d = a - b which is an integer. So (A - B) must have a factor d.

proof 2.
    given:
    A does not have a factor d.
    B has a factor d and B = bd
    we must proof:
    gcd(A-B,B) = d is impossible

    assume:
    A - B has a factor d, then A - B = A - bd = kd, where k is some integer
    dividing by d :
    A/d - b = k
    A/d = k + b
    b and k are integers, A/d is a fraction so this is impossible.
    A - B can never have a factor d.
This concludes the proof.

if A > B then repeatative application yields:
    gcd(A,B) = gcd(A - kB,B) where k is some positive integer.
    B is subtracted from A until A - kB < B.
As we will see, the Euclidean Algorithm is used to solve Ax + By = 1
where A > B , A,B are positive and have no common factors.
from these results, solutions of the original equation will be calculated.

Standardizing the equation
Back to the original equation 216x - 1000y = 4600

216, 1000 and 4600 have a common factor 8. Dividing by 8 simplifies the equation to:
    27x - 125y = 575
Look at : Ax + By = C
If A,B,C have a common factor, A,B and C can be divided by this
factor to simplify the equation.
So, from this point, we assume that A,B and C have no common factors.

If just A and B have a common factor, say d, and A = ad, B = bd, then
    d(ax + by) = C
    ax + by = C/d

C/d will be a fraction but (ax + by) is integer.
Conclusion: there is no solution in this case.

Hereafter we assume, that A and B have no common factors, so gcd(A,B) = 1.

Also, we expect in Ax + By =C that
  • A > B
  • A and B are positive


    • 27x - 125y = 575 is therefore transformed to
    27x + 125y = 575, (remember to complement y later) and to
    125x + 27y = 575, remember to swap x and y later.

General solutions
If C = 0 then Ax + By = 0 has the solutions:

    (x = B, y = -A) or (x = -B, y = A).

Say (x1 , y1) is a solution of Ax + By = C
and (x0 , y0) is a solution of Ax + By = 0 then combining

    Ax1 + By1 = C
    Ax0 + By0 = 0
    A(x1 - x0) + B(y1 - y0) = C
In general, all solutions are given by (x1 - kB, y1 + kA)
where k is some integer ...-2,-1,0,1,2,3.......

Conclusion: Ax + By = C has no solution or an infinite number of solutions.

Handling very big numbers
Back to 125x + 27y = 575

To solve this equation, first 125x + 27y = 1 must be solved.

If x1,y1 is a solution, than x = 575x1, y = 575y1 is the result we want.

This approach is not advisable because x and y may become very large, even
exceding the range of integers thus limiting the amount of equations
we are able to solve.

Therefore is it better to keep the value of C as close to zero as possible.
This can be done by subtracting(adding) A+B,A,B or (A-B) to C and introducing
correction numbers to x and y.

Instead of solving Ax + By = C we solve
    A(x-xcorr) + B(y-corr) = C - A.xcorr - B.ycorr
First, we may subtract (A + B) from C, incrementing both xcorr and ycorr,
after that subtract A from C, incrementing xcorr, then subtract B from C,
and finally subtract (A-B) from C while incrementing xcorr, decrementing ycorr.

In this way the smallest value of C is obtained.

Look at 125x + 27y = 575 again.
27 + 125 = 152, so 125(x-3) + 27(y-3) = 575 - 3*152 = 119
remembering xcorr = 3, ycorr = 3 we solve 125x+ 27y = 119
Next subtracting 4*27 from 119:
ycorr = 3+4 = 7 and we solve 125x + 27y = 119 - 4*27 = 11.
As a last step, using the Euclidean algorithm, we solve 125x + 27y = 1 and
multiply the answer by 11 to find interim values for x,y.

Hereafter, for the final answer, correction numbers, swaps and complements along
the route have to be remembered.

Solving Ax + By = 1
Using the Euclidean algorithm, we calculate gcd(A,B).

    A - q1B = r1
    B - q2r1 = r2
    r1 - q3r2 = r3
    r2 - q4r3 = r4
q means quotient, r is remainer.
The process ends when r = 1, the gcd, because A and B had no common factors.
We may write the system of equations: (if r4 = 1)



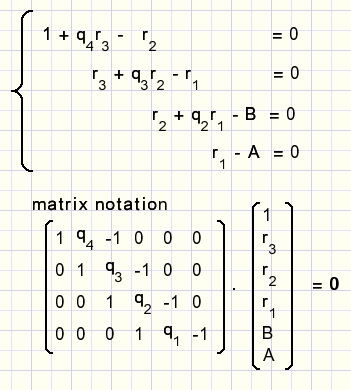
By applying elementary rules we can sweep columns 2,3,4 to zero.
After that, the vector product results:

    (
    1000-y-x
    		)(
    1
    r3
    r2
    r1
    B
    A
    		) = 0
multiplying:
    1 - By - Ax = 0
    Ax + By = 1
Now x and y have to be multiplied by C, correction factors must be added,
swaps and complements taken into account.

The original problem:



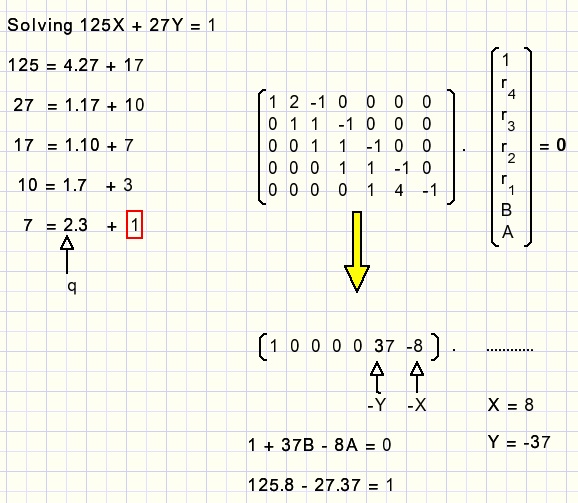
This concludes the description.

Below, I present the kernel of the program "Euclid", where Ax + By = 1 is solved.
      for i := 1 to 10 do Q[i] := 0;
  i := 0;
  repeat//calculate GCD and quotient table
   i := i + 1; 
   r := A mod B;
   Q[i] := -(A div B);
   A := B; B := r;
  until r = 0; 
  GCD := A;
  Q[i] := 1;
  if i > 2 then
   for i := i-2 downto 1 do//backward substitution
       Q[i] := Q[i+2] + Q[i+1]*Q[i];
  y := Q[1]*C+Ycorr; x := Q[2]*C+Xcorr;

Interested in the source code?

Click [here] to download the complete Delphi-3 project.

mr. Henrik Carlsen has converted this project to Delphi-10 , also changing the style to OOP
Click [here] to download this new Delphi-10 project.