best seat in a football stadium

The best seat on a tribune

This geometry problem was presented on facebook by Omid Motahed, math teacher in Beijing.

Question is:
Which seat in a football stadium is best?

Please look at the picture below:

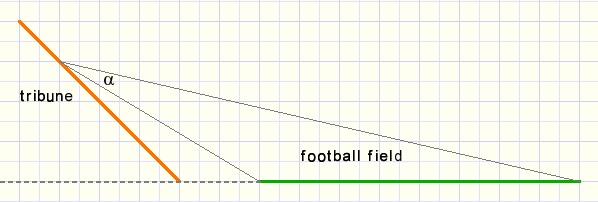
A visitor looks at the field at angle a
The bigger this angle, the better.

The solution of this geometry problem requires the lemmas of Thales, see below:

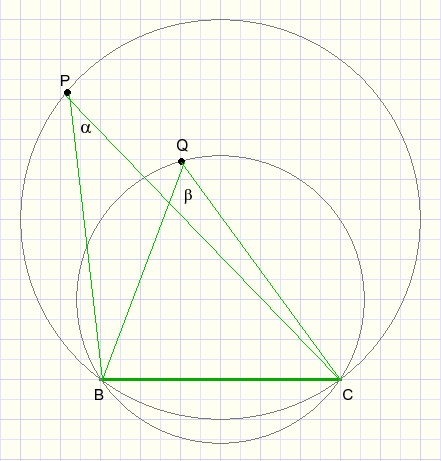
Football field BC is the chord of a circle.
Thales' lemma states that from any point on a circle we observe a chord under the same angle.
So LBPC is the same for any point P on the circle.
Also LBQC is the same for any point Q on the circle.
The smaller the radius of the circle the bigger the angle under which we observe the football field.
Please look at the picture below:

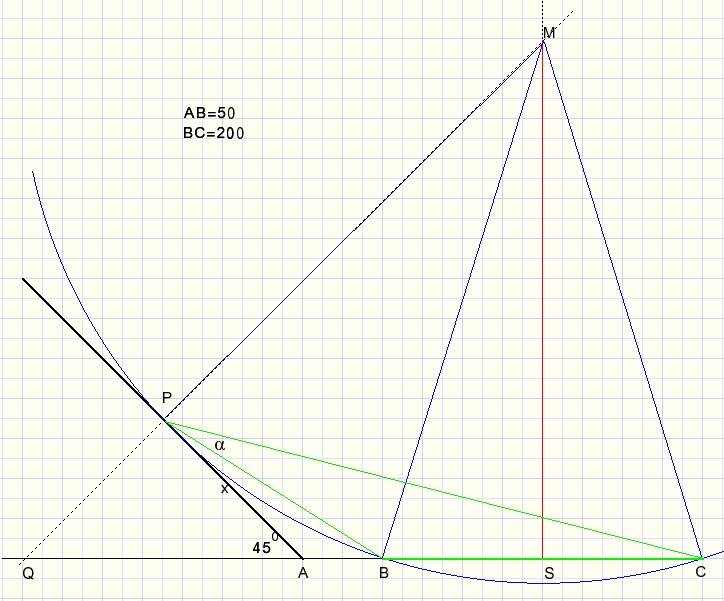
Our problem may now be redefined as:

find the smallest circle through points B,C,P This circle will have AP as tangent.

Given are:

Calculation of x = AP:

Calculation of a

Thales again:
(a chord is viewed from the circle center under twice the angle as from the circle perimeter)

⁰