The bookmark problem

Introduction

While waiting for train- or bus connections, travellers pass time by reading a book.
In most cases, these books have little value and there is no need to keep them in good shape.
Also, the book will not be finished during one period of waiting.
Therefore, the page to continue reading has to be remembered.
Three ways are available to accomplish that:
    1. pages read are torn from the book and discarded. This method is recommended for walkers.
    2. a bookmark is inserted after the page that was last read. Disadvantage : it may me be lost.
    3. the page last read is folded such, that a small triangle sticks out.
In this article we choose the third option.

The problem

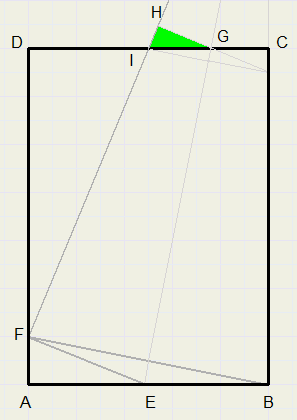Please refer to to picture right.
After folding the page, a small triangle at the top sticks out,
indicating the place to continue reading.
How must we fold to maximize the area of this triangle?
Or : how to know the length AF, given a certain width and height of the page.

Note:
EG is the folding line.
Point B folds over F, C becomes H.

BE = EF
CG = GH

What to do?

This problem carries the danger of getting stuck in endless calculations.
A good strategy is of major importance.

We assume that the Pythagoras lemma is needed as well as the theory of similarity of triangles.
We extend edge BC and folding line EG to make triangles.
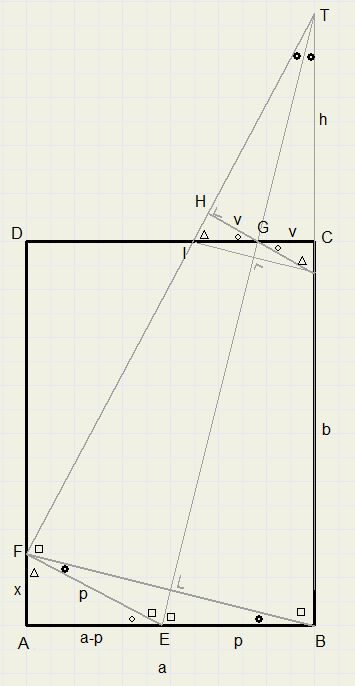For convenience we define
    AB = a
    BC = b
    AF = x
    BE = EF = p
    TC = h
    CG = GH = v
Markers denote equal angles.
(calculations left to the reader)

Final goal is a formula that expresses
the area of triangle GHI in x,a and b.

The sign ~ means similarity.
The area of triangle GHI is written as [GHI]

The strategy

p may be calculated from width a and x.
DTBE ~ DBAF, so: h may be calculated
DTCG ~ DTBE, so: v may be calculated

DGHI ~ DEAF
Define f = v : AE, then
[GHI] = f2[EAF],
because the ratio of areas of similar triangles is
the squared ratio of similar edges.

Calculation of p

Pythagoras lemma in DEAF



Calculation of h

DTBE ~ DBAF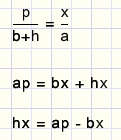



Calculation of v

DTCG ~ DTBE



multiply by x



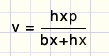
replace hx by ap - bx



Calculation of f




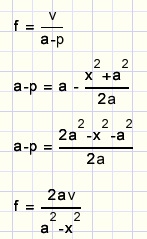
v substitution:



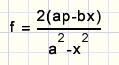
p substitution and simplifying



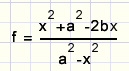
The area of triangle GHI

[GHI] = f2[EAF]
[GHI] = f2x(a-p)/2
f, a-p substitution and simplifying



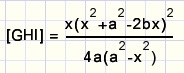
If x=0 the area is zero, which is correct.
x=a is not possible.
If folding line is CE, we notice p:b = x:a, so ap = bx and f = 0

The maximum area

Differentiation is not advisable, because a polynomial of degree 5 will result.
We feed the formula to Graphics-Explorer, and call the area y
    y = x(x^2+a^2-2b*x)^2 / (4a(a^2-x^2))
also we make a = 12 and b = 16
and select autoplot and replace
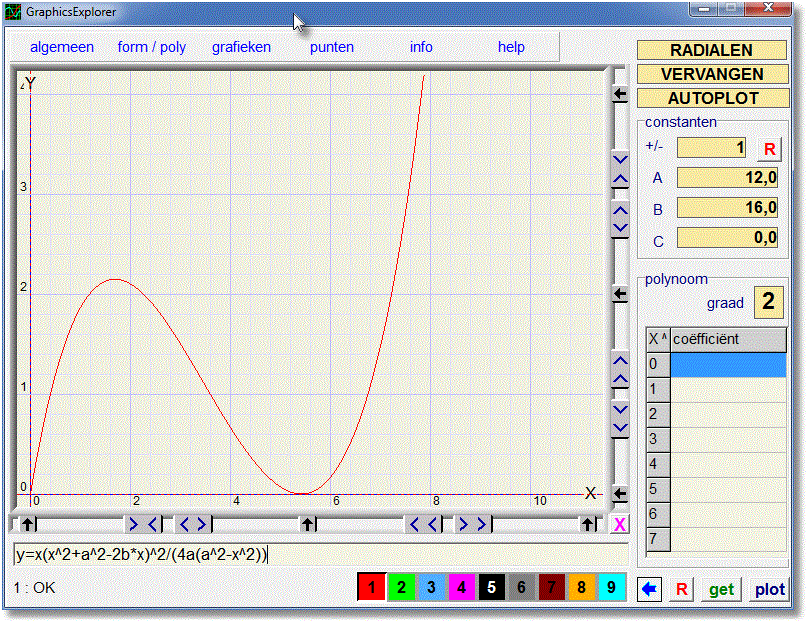
The graphic shows that y = 0 if x = 0 or x = 5,44
The maximum occurs at x = 1,72