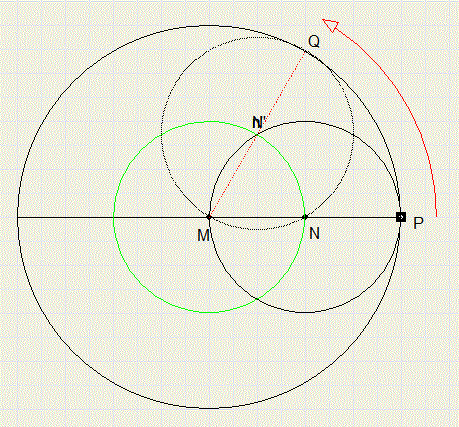
the crazy circle illusion Picture below shows two circles with centers M and N. The smaller circle touches the bigger one inside and has half the diameter. The smaller circle rolls inside the bigger one without friction. Center N moves over the green circle. After rotation, N is moved to position N'. The circles now touch in Q. Question: which way does P travel if it is fixed to the small circle? In the picture above line MN is rotated to MN', we call this angle v. This implies an arc on the bigger circle of vp/180 degrees, if the radius is 1. The smaller circle has half the radius, so it's rotation will be double the angle: 2v degrees. Rotation is clockwise. The new position P' of P after rotation is the sum of two rotations: 1. center N to N', by v degrees counterclockwise 2. 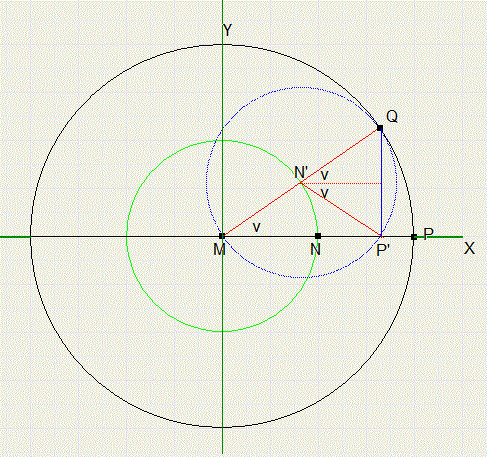point P on the smaller circle, by 2v degrees clockwise MP' = MN' + N'P' Now look at the picture below The new position of P on the X-scale becomes : X = 0,5cos(v) + 0,5cos(-v) = cos(v) The new position of P on the Y-scale becomes : Y = 0,5sin(v) + 0,5sin(-v) = 0,5sin(v) - 0,5sin(v) = 0 Conclusion: P moves over a straight line through center M. On the web you may find this nice movie named the "crazy-circle-illusion". You just read the explanation.