a connect4 search algorithm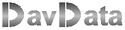e

a Connect4 search Algorithm

For the complete Delphi project and source code look [ HERE ]

contents

Introduction
The game
Coding the Board and Moves
What is a node
Winning and Losing
Replacing Drabness by Variation and Surprise
Speeding Up
Shortcut 1
Shortcut 2
Rating and Treshold
Reduced Column testing
Recognizing previous board states
The analyse button
Strategy
Summary of variables

Introduction
This document describes how my computer program CONNECT4 (version 4.0)
calculates the best move.
(To download the game, please go to the English homepage of this website)

My work on CONNECT4 started in 2001. The first ideas for an algorithm
came up while working on solutions of Peg-Solitaire.

After the first working example I kept wondering how to speed up the search process
to look further ahead within acceptable time and how to make the computer
a more interesting player.
These additions to the basic algorithm will be described as well.

In the current version 4.0 the search process has two distinct steps:

1.	A qualitative analyses of the board, looking just one move ahead. This analyses results in a recommended move for
2.	A quantitative (brute force) approach, which tries to find a better move than the one recommended.

The result of step 1. is influenced by the selected Strategy.
In step 2, the search depth is 2*level+1.

The Game

reduced image:

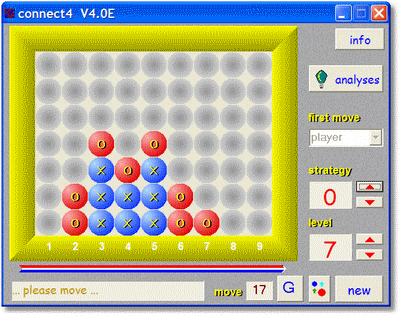
My version of CONNECT4 is single player, you play against the computer.
The board has 9 columns and 7 rows, resulting in 63 fields.
Computer and player alternately place a ball of their color in a field.
The computer always plays with red, the player with blue.
The columns are filled bottom-up, so the balls are actually dropped down
a column.
The winner is the first to achieve a horizontal,vertical or diagonal line
of 4 balls of his color.

Coding the board and moves
The game has 63 fields, each of which can be can be:

Array BORD[1..9,1..7] holds the boardstate.(BORD is Dutch for board as you guessed)
BORD[2,3] := 1 places a red ball in column 2, row 3.
BORD[4,7] := 0 removes the ball of column 4, row 7.
These moves are not visible to the player. The computer is trying moves to
find the best one and only this best move will finally be visible on the screen.

Variable KOLOMHOOGTE[1..9] (dutch for column height) holds the number off balls
already present in a column.

To find the best moves, the computer should do many alternating red and blue
moves.
ZET[1..20] holds these moves.(ZET is dutch for MOVE)
A move is a number 1..9, the selected column.
ZET[1] is the first trial move (red, computer),
ZET[2] is the second trial move (blue, player).
If ZET[3] has not been played yet then ZET[3] = 0.

Odd moves are red (computer), even moves are blue (player).

ZET[1..20] , the list of moves, is a 20 digit counter,
where each digit counts 0..9.
For level 2, where the search depth is limited to 5, only ZET[1..5] is used.
By counting from start -00000- to finish -99999- while registrating winning
and losing conditions, the best ZET[1] can be choosen.
Counting is done in the following way:

After each move, the variables BORD and KOLOMHOOGTE have to be updated
to reflect the new boardstate.

In the situation above, we assumed that no winning situation occurred and
column 1 had enough space to hold the balls.
If a column is full, the next column is choosen.
If the number of moves done is the maximum number allowed, the next step is
to take this move back and choose the next column.
Writing a sequence of moves as digits from left to right and indicating
consecutive counts by ... , the way of counting is: (for level 1, search depth=3)

000, 100, 110, 111, 112, 113..119, 120, 121..129, 130, 131..139,......., 900..999
the end of the search.

What is a Node
In mathematics, a Graph consists of a collection of dots, which may be (or not be)
connected by lines.
Graphs are abstract constructions to describe processes like competitions,
industrial planning or games.
A distinct type of graph is the Tree Graph. These graphs have no isolated dots,
travelling from dot -A- to dot -B- and back is only possible by the same lines,
(no loops exist) and removing a single line would isolate part of the dots.
These graphs look like a tree with branches, hence the name.

We use the tree graph to represent the CONNECT4 search process.
A dot is called a NODE.
This node is simply a collection of numbers of which one is the line (= move, columnn)
selected to the next node in the tree.

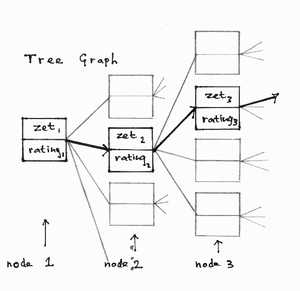
Playing at higher levels, the tree may have millions of branches, but only one branch
at the time can exist: a row of nodes connected by single lines.

Node 1 holds the first (trial) move of the computer and node 2 is the next move,
representing the player. The highest node is 2*level+1.

A node also holds a number called RATING, which indicates winning or losing conditions.
The higher this rating, the more succesfull the node is.
The general idea behind the search process is: every node tries to obtain the highest
possible rating for itself.

During the search process nodes are added / removed as moves are done or taken back.
An existing node never decreases its rating. As we shall see, only node -1- has to
remember the column for which the highest rating was achieved.

Node 1 has an extra variable called BESTZET. Before the search starts, BESTZET is
set equal to the first move of node 1.
If RATING[1] increases, BESTZET is set to the move (column) of node 1.
At the end of the search, BESTZET is the move the computer will show on the screen.

Winning and Losing
After each move, a test should be made to see if somewhere four balls
of the same color are horizontally, vertically or diagonally connected.
Say, such a situation was found at node 10 (even, a player move). Than node 9
is losing in 1 move, while node 8 is winning in 2 moves.
To win in 3 moves is better then to win in 5 moves. To lose in 2 moves is
worse than losing in 6 moves. With this considerations in mind, the variable
RATING[1..20] was choosen as shown below:

rating	meaning for NODE n
20	winning at move n (this node)
19	winning at NODE n+2
18	winning at NODE n+4
17	winning at NODE n+6
...	.............
10	neutral, no win or lose situation
...	.............
3	lose in 5 moves = win at NODE n+5
2	lose in 3 moves = win at NODE n+3
1	lose in 1 move = win at NODE n+1
0	no rating available yet

RATING[n] is indicating the success of move n. The higher the better.
Variable RATING[] obtains its value in two ways:
1.
Initially RATING is set to -0- which means that the rating is yet unknown.
When the highest NODE (n) finds no win, RATING[n] is set to 10, the neutral
rating.
2. When a win is found at NODE n, RATING[n] is set to 20, the highest rating.

When the ZET[ ] counter = 340, meaning that for move 1 column 3 was choosen,
the next move was in column 4 and move 3 was not yet done, this means that
now node 3 must be added.
When ZET[ ] = 349, node 3 must be removed, next ZET[ ] = 350, node 3 is added again,
ZET[ ] becomes 351,352...etc.

When closing (removing) node n and going back to node n-1, the new rating for
node n-1 is calculated using the following rules:

x := 20 - RATING[n]
if x < 10 then x := x + 1
if x > RATING[n-1] then RATING[n-1] := x

Summarizing:
OPEN (adding) a node n includes:

BACK

OPEN

BACK to previous node n-1:

NEXT move:

This describes the search algorithm. The program can be built, the game
played.
However, it is utterley boring. The computer prefers column 1, or else column 2.
The most common rating is 10 and this rating is allready obtained
by move 1 in column 1 in most cases. BESTZET=1 is this case.
Added to that: the search proces is very slow at search depths > 8.

Replacing Drabness by Variation and Surprise
A node performs moves sequenced 1..9. Column 1 is the first selected.
But to make the game more surprising, we choose a random column, say 5,
to start with. Now each node counts the columns 5..9,1..4
When no win is found, BESTZET will be this random column.
Before each search, a new random column to start with is choosen.
Now we observe alternating apparent smart and stupid computer-moves.
This is the way the -RANDOM- strategy works.

Speeding Up
1.
Much time during the search process is spend testing for a line of four balls
of the same color.
As we noticed, BORD[ ] is a 2 dimensional array. Since the computer memory is a
1 dimensional array (of bytes), for each field with column c and row r,
a small calculation is necessary to know the place of BORD[c,r] in the
computer memory.
This calculation may be eliminated by defining a 1 dimensional array BORDX[..]
at the very same memory locations as BORD[ ].
If p = 9*c+r , then BORDX[p] is the same memory location as BORD[c,r].
Adding 9 to p selects the field to the right, subtracting 8 from p selects the
field left below.

2.
When a node wins, this node closes and the search process continues at the
previous node. All branches of a winning node are skipped.
The lower the node, the more time is saved in this case.
So, it is favourable to detect a win as soon as possible during the search.
This is done in the following way:
after a node opens (is added) it tests all columns 1..9 for a possible win
before a move is done and the next node is opened.

3.
Testing for a win can be shortened in another way as well:
instead of adding a ball to a column and testing for a line of 4 balls
of the same color, we calculate if a move in a certain column would
cause a line of 4.
In this way, the move (plus it's removal) is no longer necessary in case 2. above
and in the last node.

4.
While scanning the board for a line of 4 a test must prevent crossing the edges.
However, this test is not necessary if we add edges of "0" around the board.
Reaching an edge now detects a "0" (empty field) and the scanning for that direction
will stop.
So, BORD[1..9,1..7] becomes BORD[0..10,0..8], BORDX[1..63] becomes BORDX[0..98].

5.
In the random strategy, each node counts the columns starting at a random column,
the STARTKOLOM, say 7, so the counting sequence is 7,8,9,1,2,3,4,5,6 in this case.
The search process is speeded up by about a factor 4 if each node's startcolumn is
1 column higher than the previous node's startcolumn.(8,9,1,2,3,4,5,6,7)
A variable STARTKOLOM[ ] is added to each node. The values are calculated at the
start of the search.

All these measures however are marginal compared to the SHORTCUTS.

Shortcut 1
Consider the following case:
The rating of node 4 is equal to 10.
Node 5 just obtained rating 10, so RATING[5] = 10 and node 5 has only done part
of all moves.
Node 5 may select the next move in an effort to increase it's rating. However,
this action is of no influence to the rating of node 4.
If node 5 reaches a rating of say 16, then x := 20-16 + 1, x := 5.
This is less then the rating of node 4, which will therefore not be changed.
So, it is unnecessary for node 5 to perform any more move, opening a next node.
Node 5 can be closed and node 4 continues the search to increase it's rating.
If this (shortcut) takes place in the lower nodes, incredible time may be saved.
Millions of moves are skipped.
This is the most important time saving measure.

Shortcut 2
The two highest (deepest) nodes behave differently.
The last (deepest) node can only have a rating of 20 (win) or 10 (neutral).
The previous node to this thus can have the rating 1 (lose in 1 move) or
10 (neutral).
So, this node must be closed when reaching a rating of 10.

Rating and Treshold
To sense a shortcut1 situation, ratings of the current- and previous node
must be compared.
However, we may "transport" the rating of node n-1 to node n, calling this number
the TRESHOLD.
So, a variable TRESHOLD[ ] is added to each node.
After opening node n+1 this happens:
x := 20 - RATING[n]
If x > 10 then x := x + 1
TRESHOLD[n+1] := x
Now, a node is closed (all moves not yet done skipped) if the rating of the
node reaches or exceeds it's treshold.
Opposite to the rating, the treshold of a node may only be decreased.

Node 1 starts with a treshold of 20 and a rating of 1. (only closes on win)
If a node does not detect a win in any of it's columns after opening, a treshold
of 20 is decreased to 19.
The 2 last nodes start with a maximum treshold of 10.
If a node has performed all possible moves, than the treshold is set equal
to the rating only if this causes a lower treshold.

Summary
Opening node n:

Closing node n:

Example 1:
(search depth 10, no win found yet)

node	8	9	10	situation / remarks
TRESHOLD	19	10	0	node 9 did not detect win and opens node 10
RATING	1	1	0	node 9 did not detect win and opens node 10
TRESHOLD	19	10	10	node 10 did not detect win and closes
RATING	1	1	10	node 10 did not detect win and closes
TRESHOLD	19	10	10	node 9 closes because treshold = rating
RATING	1	10	10	node 9 closes because treshold = rating
TRESHOLD	19	--	--	node 8 performs next move, opens node 9 etc.
RATING	10	--	--	node 8 performs next move, opens node 9 etc.

Example 2
(previous win in node 7, node 3 rating indicates win at 4 moves ahead)

node	3	4	5	situation / remarks
TRESHOLD	19	--	--	open node 4
RATING	18	--	--	open node 4
TRESHOLD	19	2	--	open node 5
RATING	18	1	--	open node 5
TRESHOLD	19	2	20	--
RATING	18	1	19	--

If node 5 does not detect a win, then it's treshold will be lowered to 19.
Since the treshold is now equal to the rating, node 5 will close.
For node 3, a win in node5 is the only opportunity to increase it's rating,
since earlier a win occurred in node 7.
Again many moves are eliminated.

Reduced Column testing
Immediately after opening, a node tests all the columns for a possible win.
Since a win was not detected in the nodes before, such a win can be the result
of:

So, in node n+2 it is impossible to sense a win in columns that are more than
3 columns apart from the move of node n.
As a result of the move in node n+1, only a win in the same column is possible.

A variable COLCHECK[ ] is added to each node. Bit c of COLCHECK[n] = 1 if
this column needs to be tested for a win.
After the column is checked, the corresponding bit is reset.
Node n sets COLCHECK[n+2] to the right value.
The column selected by the previous node is unconditionally tested for a win.

Recognizing previous board states
Different sequences of moves may result in the same board state.
examples are:

Equal board states will produce equal ratings.
When a board state reappears, its rating may be remembered and subsequent
moves in the search tree may be skipped.
A problem however is that recognizing previous board states takes much
processor time.
This time must be subtracted from the time saved. Because of shortcuts, the
actual time saved is somewhat uncertain.
Therefore, limitations are incorporated to keep things simple.

Consider 3 consecutive moves. There are 9*9*9 = 729 of such sequences.
Identical board states are produced by sequences of the type 1,2,3 ... 3,2,1
or in general : a,b,c .......c,b,a.
Of this type , 9*8*7/2 = 252 sequences have twin board states.
Thus, in the most favourable situation, we may save 252 moves (and remainder of tree) out of 729,
which is 35%. This may occur in each node >= 3.

Now consider 4 consecutive moves.
All sequences leading to a duplicate board state have the form 1,1,2,2 ..... 2,2,1,1
in general a,a,b,b ..........b,b,a,a
Every other node may detect such a situation.
There are 9*9*9*9 = 6561 sequences of 4 moves of which 9*8/2 = 36 may cause
identical board states. We will not waste time on sequences of 4 moves.

So, here is the method used by CONNECT4 version 4.0 to recognize previous board states
considering three consecutive moves only.

First a description of the variables.
Each node, starting at 3, has a variable Q3MapAddr which holds the hexadecimally coded
3 consecutive moves.
If zet[5] = 3, zet[6] = 2 and zet[7] = 9 then Q3MapAddr[7] = $0329.

Table Q3Map[$111 .. $999] has an entry for every possible sequence of 3 moves.
The table is built when the game is opened first.
If a sequence of three moves is of type a,b,c then Q3Map[$abc] and Q3Map[cba] are set to a same
unique number in the range 1..252.
Other entries of Q3Map are set to zero.

Each node has a table, QReg, of 252 entries of the following record:

The score field of node[n] holds the rating which is calculated when node[n+1] closes,
if the moves of nodes n-2,n-1,n where of type a,b,c.

Each node also has a variable Q3Key, which is a LongInt integer.
Q3Key[n] is stored in Q3Reg[n,i].lock when node[n] sets the score field of Q3Reg[n,i].

The key and lock variables form a validation mechanism.
On a new move of node p, Q3key[p+3] is incremented so all Q3 entries for node p+3 are invalidated.

To register a rating for future reference, following actions take place:

To recognize and use a previous board state and it's rating :

Measurements show, that over 99% of cases where the key and lock values compare,
a move (and subsequent tree branches) are skipped.

This concludes the description of the -brute force- search process.

The analyse button
With the analyze button pressed, the computer shows a prediction
for each column choosen next by the player.
To accomplish this, in a table the tresholds for each column of node 3 are stored.
Node 3 must be disabled to make shortcuts, which is done by setting TRESHOLD[3]=20
upon opening of the node, regardless of the rating of node 2.
The search process is slowed down about 2.5 times.

Strategy
When strategy 0 is selected, the search process is as described before.
If no win is detected, seemingly smart and stupid computer-moves are noticed.
This generates vivid games, but the moves lack cohesion.
"Strategy" is added to give the computer a distinct style for the price of
a more predictable response.

When selecting a strategy > 0 , the computer starts by a trial move in a column
followed by an analyses of the board state. The result is a score.
The column with the highest score is presented to the -brute force- quantitative
search as STARTKOLOM[1].
The quantitative search tries to find a better move then this one.
If no win is found, BESTZET = STARTKOLOM[1], the actual computermove.

A different strategy uses a different algorithm to calculate the score.
The following is done:
A possible line of 4 balls on the board is called a street.
A board of 9 columns and 7 rows has 126 streets (just count!)
A type is assigned to a street:

A (street)value is generated for each street.
The streetvalue is simply the number of balls (0..3) placed.

For each empty field, 2 values are calculated:

The strategy is a 3 bit number. The contribution of each bit to the score is:

xx1 :	score := score + 2 * sum of all streetvalues of type 1 streets
x1x :	score := score - 2 * sum of all streetvalues of type 2 streets
1xx :	increase value of a field with value of field just above for each field on distance 2: score := score + 3 * fieldvalue
1x1 :	score := score + sum of all fieldvalues 1
11x :	score := score - sum of all fieldvalues 2

Style and strategy:

The influence of the strategy on the game decreases at higher levels.

Summary of variables

n	byte, indicate number of node
BORD[0..10][0..8]	array of 11*9 bytes, holds board state, borders are -0-
KOLOMHOOGTE[1..9]	number of balls in this column
STARTKOLOM[1..20]	first trial move for node 1 .. 20
ZET[1..20]	byte, the move of node 1 .. 20
BESTZET	byte, holds best move of node 1
RATING[1..20]	current rating of node 1 .. 20
TRESHOLD[1..20]	highest rating possible for node 1 .. 20
COLCHECK[1..20]	16 bit word, bits 1..9 indicate columns to be tested for win
Q3MAP[$111..$999]	729 entries, 1 for each -3 moves- sequence.
Q3MAPADDR[1..20]	16 bit word, hex encoded last 3 moves of nodes n-2, n-1, n is index into Q3Map
Q3REG[1..20,1..252]	record: lock,rating. 252 entries per node
Q3Key[1..20]	long (32 bit) integer, validation number for each node

This concludes the description of my CONNECT4 search algorithm.