Energy Storage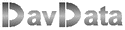

This article may be viewed best with IE or Chrome.
Other browsers do not display all formulas correctly.

Introduction
For several reasons, western countries want to decrease their dependency on oil.
Alternatives for oil are:
    windmills
    solar cells
    thermal solar heat collectors / solar towers
    methanol production from agricultural waste
    nuclear energy
    hydroxen (liquid or gas)
In the case of windmills, solar collectors or solar panels a problem arises:
sunshine and wind are variable to a high degree.
During favourable conditions, excess energy must be stored to survive periods of shortage.

This article focusses on some possibilities to buffer energy.
I promise interesting comparisons, especially by adding the energy-densities of different solid fuels and
uranium used in nuclear power plants.

Not accounted for are (maintenance) costs and efficiency of the systems.

Motivation for this small study was an article stating that the world's total need of electricity can be met
by a solar collector system occupying the area of France in the Sahara desert.
In such a thermal solar power plant sunlight is projected on tubes containing water.
Water is heated to steam which drives turbines and generators.
Electricity is transported by wire to the consuming countries.
Every city or houshold however should buffer an amount of energy for at least a few days to
survive cloudy days, malfunctions or terrorist attacks.

The following storage systems are considered:
    electrical / chemical : batteries
    mechanical : potential energy
    mechnical : kinetic energy
    pneumatical : pressured air
Objective is to store an amount of energy sufficient for one household for one day..

Energy in general
Energy is what causes change or movement:
    electrical : moving electrons
    mechanical : moving matter
    thermal : oscillating atoms
    chemical : binding energy of atoms
Energy is never lost.
One type of energy may be transformed into other types:
    chemical to electrical : battery
    electrical to mechanical : motor
    mechanical to electrical : generator
    chemical to thermal : combustion
    thermal to chemical : growth of plants

The unit of force is Newton.
1 Newton accellaretes a mass of 1 kg. by 1 m/s2 (in case of no friction).
A mass of 1kg. on earth experiences a gravitational force of 9,8 Newton.

The unit of energy is Joule.
In the case of mechanical energy:
If a force of 1 Newton moves an object over 1 meter, the required amount of energy is 1 Joule.
This energy is lost as (friction) heat.

Energy E = F.d (Joule) if a force F moves an object over a distance d.

Energy per second is called power.
If a constant power is used during s seconds, the total energy
    E = P.s
    P = E / s.
The unit of power is Watt. 1 watt = 1 Joule / second.
Because 1 Watt is very little power, the power of electric stoves or motors is indicated in kiloWatt (kW).
But 1 kW during 1 second is still a small amount of energy.
Electric companies therefore count in kWh, kiloWatt * hours. so,
1 kWh = 1000*3600 = 3,6MJ.....{3,6 mega-Joule}

The average use of a household in the Netherlands is : 10kWh = 36MJ per day.

Liquid fuels
One liter gasoline produces 30MJ when combusted, so a household would need a tank of 1,2 liters daily.

The energy-density of methanol is only little less: 2 liter is needed for 36MJ of energy.
Methanol may be produced from agricultural waste.
It may be used in fuel cells to generate electricity.

Liquid hydroxen has an energy-density of 8,4MJ / liter.
This seems interesting but problems are big: it can only exist near absolute zero,
about 270 degrees Celsius below zero.

Batteries
The best type of rechargable battery is Li-ion, having an energy-density of 0,1kWh/kg = 360kJ/kg.
So, a battery of 100 kg. is needed to survive a cloudy day without a breeze.

Gas
Vapoured hydroxen under pressure of 200 bar has an energy-density of 1,9MJ / liter,
this is 16 times less then gasoline.
So for one day, a tank of 19 liters is needed.
Compression needs much energy.

Natural gas consists for 90% of methane. The energy-density is 35MJ/m3.

Potential energie
This is the principle of the cuckoo-clock : a lifted weight.
In our home we build a shaft in which a large weight can move up and down.
    potential energy

When a mass m (kg) is lifted h (meter), the required energy is
    E = m.g.h
where g = 9,8 m/s2, the accelleration of gravity on earth.
In case of a concrete block of 1 m3 lifted 10 meter and
a density of the concrete of 2500kg/m3 the total energy amounts:
    E = 2500.9,8.10 = 245kJ.

So 147 blocks are needed to supply the energy for one day.
A 1kW vacuum cleaner can be operated for 245 seconds or little over 4 minutes
before the block reaches the ground.

A nice thing is that the position of the block immediately shows the possibilities for the rest of the day:
in case of downward movement one is discouraged to switch on the flat-iron.

Kinetic energy
This is an application of the flywheel.
Flywheels are used to bridge a short power loss.
In this time, a diesel generator can be started.

    flywheel

We calculate the energy of a flywheel and start with the formula for the kinetic energy
of a mass m moving at v (m/s):
    E = 
    1
    2
     m v 2
Problem : the speed depends on the distance from the center.
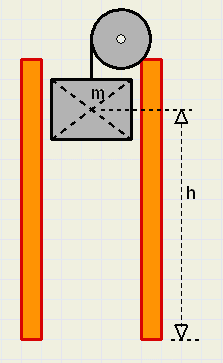
We consider a small concentric circle with radius r and width Dr.
(green in figure above)
Because the width is very small, every point has the same speed.
The material has a density of r (kg/m3).
The thickness of the wheel is d (meter).
The mass of the layer at distance r from the center is :
    Dm = 2pr.d.Dr.r

At n revolutions per second the speed is, at distance r from the center :
    v = 2pr.n

combining, the kinetic energy of the layer is :
    DE = 4p3drn2r3Dr
so
    E = 4 p 3 d r n 2 
    ó
    õ    		r 3 dr
    E = p3drn2R4....integrated over 0...R
However, the mass of the complete wheel is
    M = pR2rd
which simplifies the formula
    E = Mn2p2R2
    E = M(pRn)2
The speed at the perimeter is
    v = 2pRn
so
    E = 
    1
    4
     M v 2
The density of concrete still 2500 kg/m3, we install a concrete flywheel with radius 1 (m) and thickness 0,25m.
The number of revolutions is 25 / s.
The amount of stored energy is in this case:
    E = 0,25 . 3,14 . 0,25 . 2500(2 . 3,14.25)2 = 12MJ.
Not bad!
We can operate the vacuum cleaner for over 3 hours.
Unfortunately a lot of noise must be taken for granted: devices like this simulate a thunderstorm.

Pressured air
Recently the press reported of cars being moved by compressed air.
Time to investigate the amount of energy in a cilinder holding compressed air.

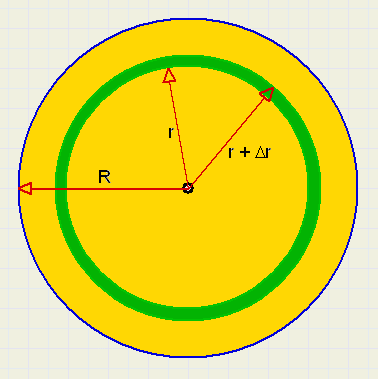
We consider a very long cilinder where a piston compresses the air as it it forced inside.
    compressed air

The cilinder is open at the right side and closed at the left side.
When x = 0 the pressure at both sides of the piston is the same : 1 bar.

When compressing a gas at constant temperature the physics law is : pressure * volume = constant.
The piston area is A (cm2), so the volume of the cilinder
    V = A.L
    PV = AL
Now the piston is moved left inside the cilinder, which requires increasing force.
At position x, the volume of the compressed air is
    V = A(L - x)
and because PV = constant = AL :
    PV = A.L
    PA(L - x) = AL
     P = 
    L
    L − x
P - 1 is the pressure difference on the piston, so the force F required is
    F = (P-1)A
    F = A 
    æ
    L
    L − x
     − 1    		ö
    ­­
    èø
     = 
    A x
    L − x
If the piston moves very little, Dx , beyond x, we may consider F a constant
The required energy for this motion is:
    D E = F D x = 
    A x
    L − x
     D x
and the total energy over 0 ... x is
    E = 
    ó
    ô
    õ
    A x
    L − x
     dx
Let us introduce u such that
    u = L - x
    x = L - u
and the formula changes into
    E = 
    ó
    ô
    õ
    A (L − u)
    u
     d(L − u)
    E = A 
    ó
    ô
    õ
    æ
    L
    u
     − 1    		ö
    ­­
    èø
     d(L − u)
    E = A 
    ó
    ô
    õ
    æ1 − 
    L
    u
    		ö
    ­­
    èø
     du
    E = A(u - L.ln(u) + K)................K is a constant
    E = A(L - x - L.ln(L - x) + K)
if x = 0, then also E = 0, so
    K = L.ln(L) - L
    E = A(L - x - l.ln(L - x) + L.ln(L) - L)
     E = A 
    æL ·  ln
    æ
    L
    L − x
    		ö
    ­­
    èø
     − x    		ö
    ­­
    èø
and because V = AL :
    E = V 
    æ ln
    æ
    L
    L − x
    		ö
    ­­
    èø
     − 
    x
    L
    		ö
    ­­
    èø
In this formula some dimensions are wrong.
The piston area was measured in cm2, 1 bar of pressure causes 1 kg = 10N force per cm2
which is a force of 100.000N per m2
Measuring the piston area in m2 changes the formula into:
    E = 10 5 V 
    æ ln
    æ
    L
    L − x
    		ö
    ­­
    èø
     − 
    x
    L
    		ö
    ­­
    èø
L
L − x
 ....is de compression-factor (c) :
    c = 
    L
    L − x
    c L − c x = L
    L (c − 1) = c x
    x
    L
     = 
    c − 1
    c
The formula can be written as:
    E = 10 5 V 
    æ ln c − 
    c − 1
    c
    		ö
    ­­
    èø
V is the total volume at a pressure of 1 bar.
It makes more sense to indicate the volume of the compressed air, so V is changed to cV.

A cilinder containing compressed air at c bar and with volume V holds a total energy
    E = 10 5 c V 
    æ ln c − 
    c − 1
    c
    		ö
    ­­
    èø
Example:
in our loft we install a cilinder having
- a diameter of 50cm
- a length of 2 meter
- a pressure of 200 bar.

Total energy:
    E = 105 . 200 . 3,14 . 0,252 . 2 (ln(200) - 199/200) = 33,7MJ
Almost three times the energy of the flywheel.

Cilinders with compressed air may be used to increase the efficiency of cars.
At present, braking energy is lost.
Compressing air during braking stores this energy to be used on accelleration.

Solid fuels
Traditionally mankind has survived winters using wood or coal.
Table below shows the energy-densities of some solid "fuels":
    coal30MJ/kg
    dry wood19MJ/kg
    plastic30MJ/kg
    car tyres35MJ/kg
    household waste8..11 MJ/kg
    dry cowdung15MJ/kg

Nuclear energy
In nuclear power plants uranium is split, which produces heat.
The energy-density of the uranium is 80.106MJ / kg.
0,16 gram is sufficient for one household for one full year.

Science fiction
According to the famous formula of Einstein, mass itself is a form of energy :
    E = mc2
where c is the speed of light in meter/s: c = 3.108m/s

If mankind manages to transform mass into energy then 1kg. of matter produces
    90.109MJ.
1 gram of matter satisfies the energy requirements for one household during 6850 years.

Summary
To buffer enough energy per household for one day, one of the following choices could be made:
    - 1 m3 natural gas
    - 1,2 liter gasoline
    - 1,2 kg. coal
    - 1,9 kg. dry wood
    - 2 liter methanol
    - 2,4 kg. dry dung
    - 4,5 liter liquid hydroxen
    - 19 liter gaseous hydroxen at 200 bar
    - 100kg. Li-ion batteries
    - 150 blocks concrete, each lifted 10 meter
    - a concrete flywheel, radius 1,3m, thickness 0,25m, 25 revolutions/s
    - a cilinder compressed air, length over 2 m. , diameter 0,5m. pressure 200 bar
Because losses are not accounted for here, in practice more will be needed.