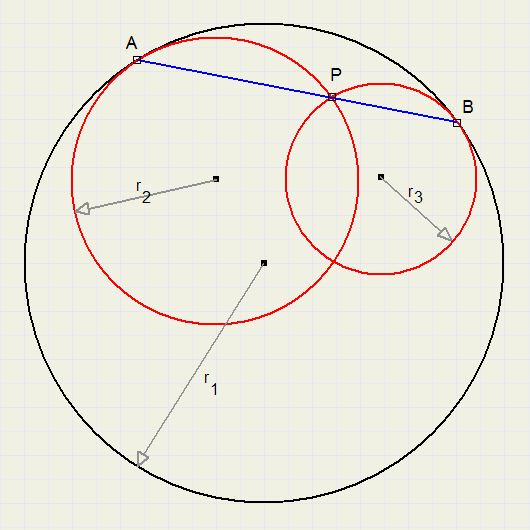
Geometry Puzzle Below, you find a nice geometry puzzle. Send your solution , with your name and e-mail address, to david@davdata.nl so I can publish it here. Solution 1 by Bruce Description Given are: - a circle with radius r1 and inside - two circles with radius r2 and r3 which contact circle 1 at points A and B - the centers of circles 1,2 and 3. - the intersection point P of circles 2 and 3 Prove the following theorem: If P is on line AB then r1 = r2 + r3 must be true success...! 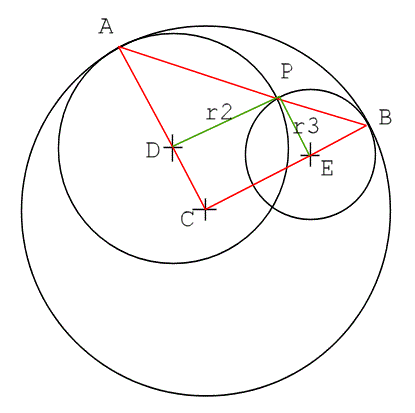Solution 1 (Bruce) The problem is to prove that line APB is straight if r1 = r2 + r3 For APB to be a straight line, we need to show that the sum of angles APD + DPE + EPB = 180 Notice that CD + AD = r1 also CE + EB = r1 But, our condition is r1 = r2 + r3 So, this means that DPEC is a parallelogram. So, CD = r3 and CE = r2 Finally, we use the parallelogram to relate angles DAP = EPB and ADP = DPE Since angles of triangle ADP sum to 180deg Then so do the angles on the line APB.