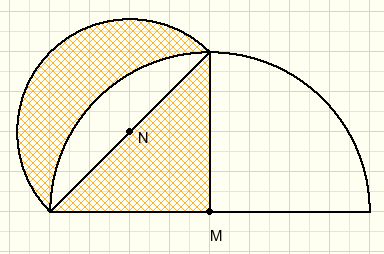
geo puzzle In the figure above the circles have centers M, N. Proof, that the marked areas are equal. A first approach would be to define the radius of circle M = 1, than calculating the radius of circle N using the Pythagoras lemma. But a simplification is possible: 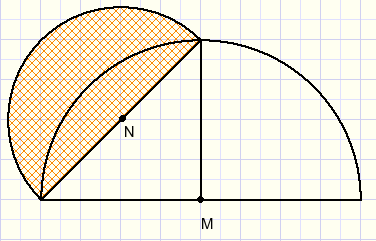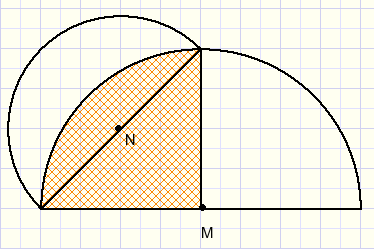We also may proof, that the marked areas in above pictures are equal. We do not need the Pythagoras lemma either. In picture below we observe that area ABCD = 2* area PQRS. 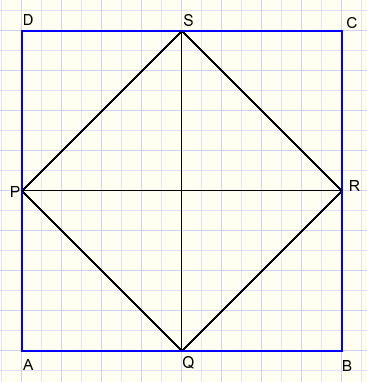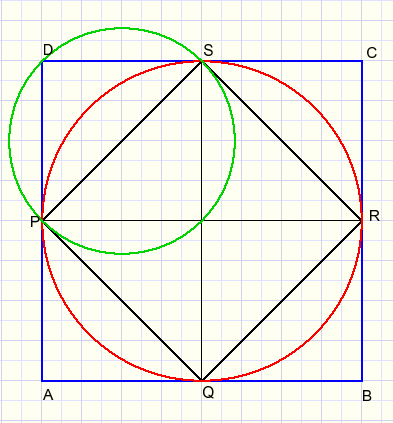Adding circles: So, the large red circle has twice the area of the small green circle. A quarter of the red circle equals half of the green circle. That concludes the proof.