

| Geometric construction problem |
This geometric construction problem was placed 14-09-2018 on facebook by Tungsteno.
The solution is my own.
Given are points A and B and a circle c.
Construct a circle through A and B that intersects c in diametrically opposite points.
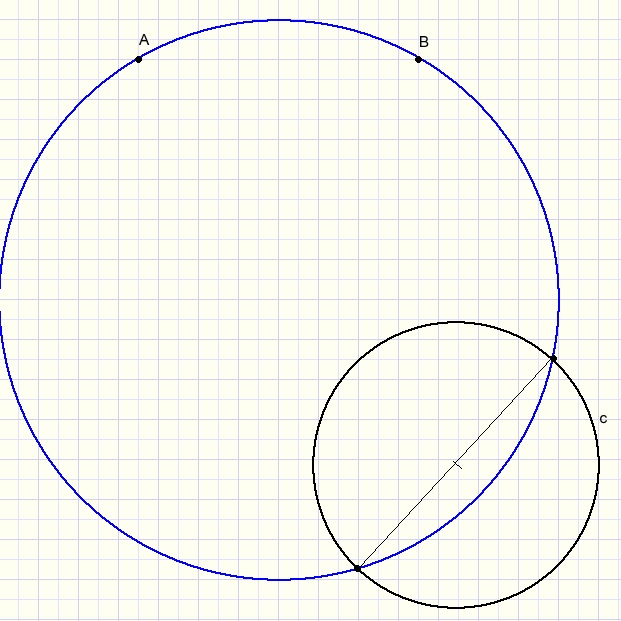
In above picture, the blue circle is the solution.
Now look at the picture below:
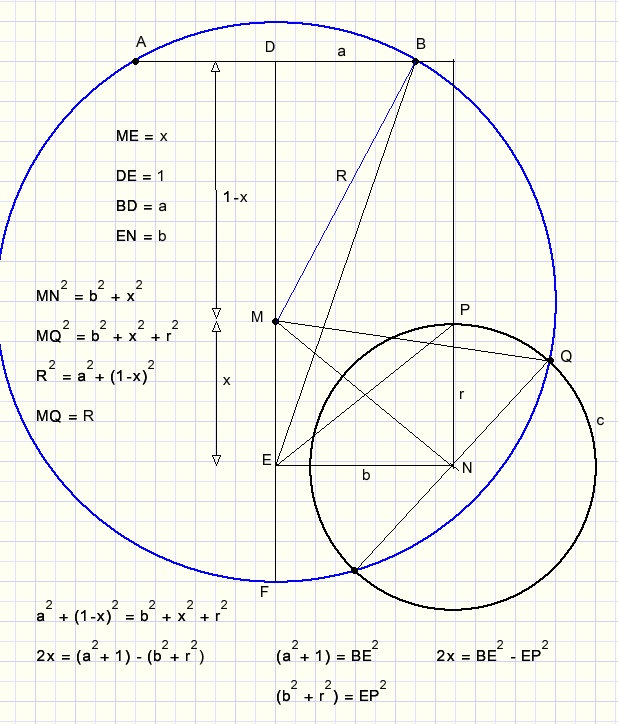
The center N of circle c we assume at distance 1 from line AB.
Center M of the circle we have to construct must be on the perpendicular bisector DF of AB.
N has distance b to this bisector.
So, 2x = BE2 - EP2.
We proceed:
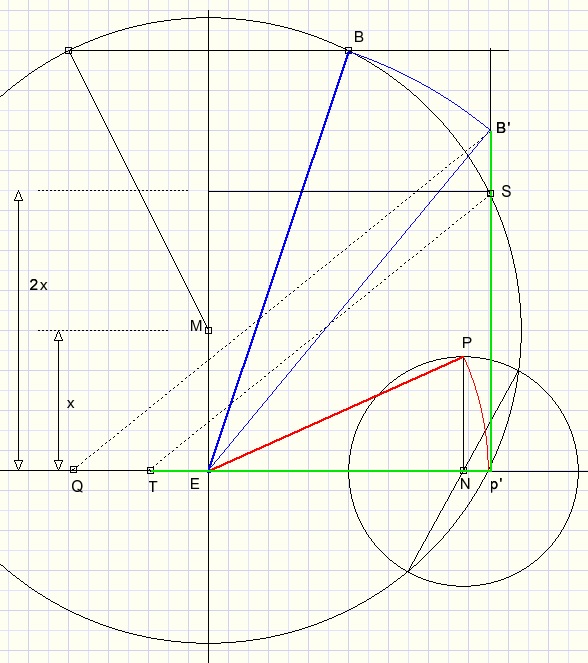
Take E as center.
Circle EP.....EP'
Draw line from P' perpendicular to EN.
Circle EB , intersection with previous line is B'.
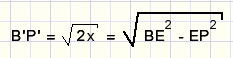
We have to square the above formula to obtain 2x.
Extend P'E such that P'Q = 1.
Draw P'T = P'B'
Draw TS parallel to QB'.
P'S = 2x
Note:

It looks like point S is on circle M.
Is this coincidence?
No, it is not.
Proof is left to the reader.
This concludes the construction.
An interesting problem.
However......
A nice thing about geometry is that logic reasoning may replace massive calculations.
In the previous solution only basic geometry rules were used together with some algebra.
In the next construction the algebra is absent because we use a powerfull lemma.
But first a proof.
Consider 1 point A and a circle.
Then many circles through A are possible that intersect the circle at diametrically opposite points (P and Q).
(just choose P and Q differently)
See picture below:
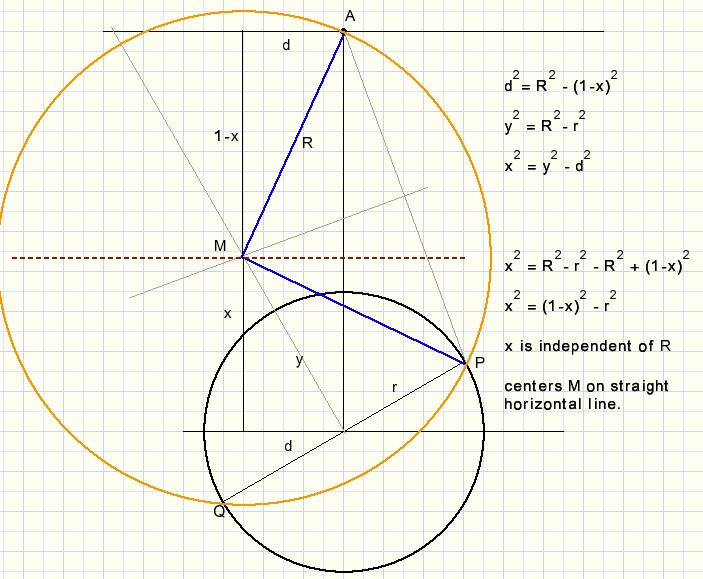
Here we assume that A has distance 1 to the circle center.
We notice that x is independent of radius R, so all centers M are on a straight horizontal line.
So, this is all algebra we need.
The new lemma is
-
If circles (M) through a point (A) intersect another circle (center N) in diametrically opposite points
than the centers (M) of these circles lay on a straight line
(perpendicular to AN)
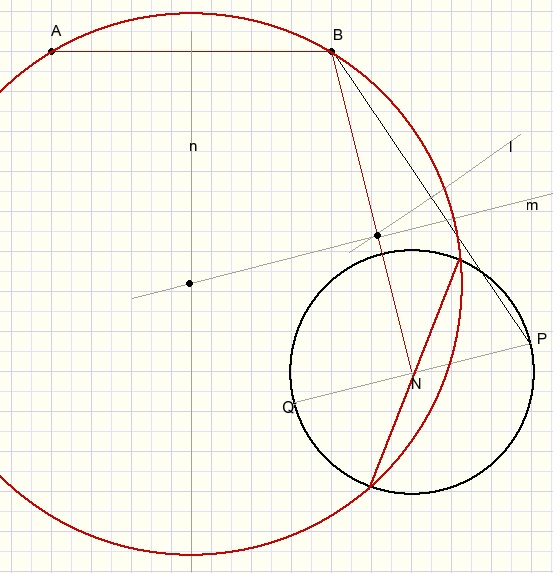
- draw BN.
- draw PQ perpendicular to BN.
- draw BP.
- draw line l, perpendicular bisector of BP.
- draw line m through intersection of l and BN parallel to PQ.
- draw line n, perpendicular bisector of AB
- center M of circle is intersection of m and n.
Note: possible circle centers are on line m.
But to run through point A, the center has to be on n as well.

