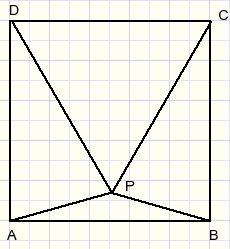
Geometry problem Please look at the next geometry problem: Given is square ABCD. Triangle CDP is equilateral. Calculate the size of LBAP. This calculation is not difficult. The result is 150. However, the reverse problem is not so easy: Given is square ABCD and point P within such that LPAB = LPBA = 150. Prove that triangle CDP is equilateral. How to start such a proof? The 150 angle does not bring us far. We have to use the fact that ABCD is a square. So let's start by reflecting ABP around diagonal AC. 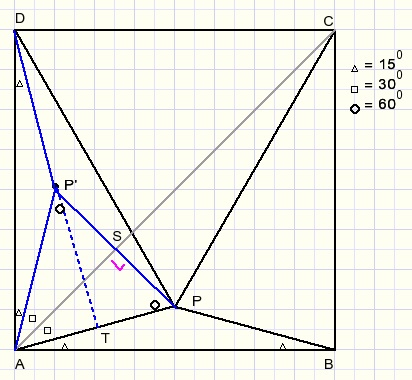Now look at the next picture, somewhat enlarged for clarity: Point P' is the reflection of P on line AC. Now focus on triangle APP'. AP = AP' and LPAP' = 90 - 2*15 = 600. LAPP'= (180 - 60)/2 = 600 so triangle APP' is equilateral. We extend line DP' to point T on AP. LATD = 180-15-15-60 = 900 P'T is perpendicular to AP and because triangle APP' is equilateral, T is the center of AP. DT is the perpendicular bisector of AP. So DA = DP. For reasons of symmetry CP = DP. Because ABCD is a square AD = CD. Triangle CDP is equilateral. There may be better, shorter of more creative solutions. Please let me know and I will be happy to publish your solution below.