Geometric problem (11)

Given is triangle ABC with inside point P. See next figure for details:



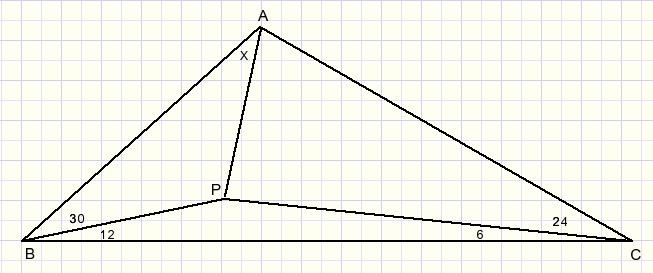
Question: the size of angle x.

Problems like this may be attacked by trigonometry: cosine and sine rules.
Just give some side a convenient value and calculate the other sides and angles.

However, the regularity of this figure (angles are 30 degrees, all multiples of 6)
suggest that a pure geometric approach might work.

This problem is not easy.
We notice point P where lines from angles A,B,C intersect.
For a start we think about a more familiar situation.
The bisectors of the angles of a triangle intersect at 1 point.
Maybe the problem can be modified to create bisectors.
Let's draw the circumscribed circle of ABC:



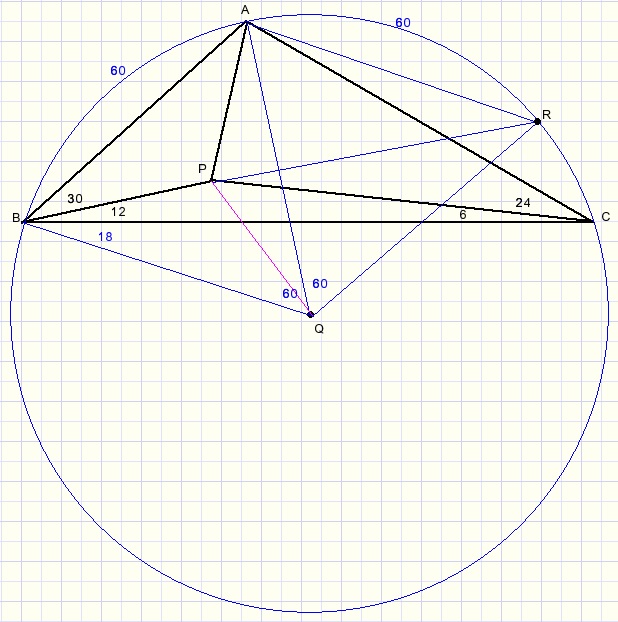
The center of this circle is Q, we draw QB, QA and QR.
R is on the extension of line BP.
Application of the Thales theorem for angles B, C reveals:
(see appendix 2 for explanation)
    - arc AB = arc AR = 60 degrees.
    - triangles ABQ and AQR are equilateral.
    - ABQR is a rhombus so AQ and BR are perpendicular.
    - PA = PQ (symmetry).
    - LCBQ = 18 degrees.
    - BP is bisector of LB.
Next we add the circumscribed circle of triangle APC.
The picture below is correct if LPAV = 90 degrees,
in that case PV is diameter.



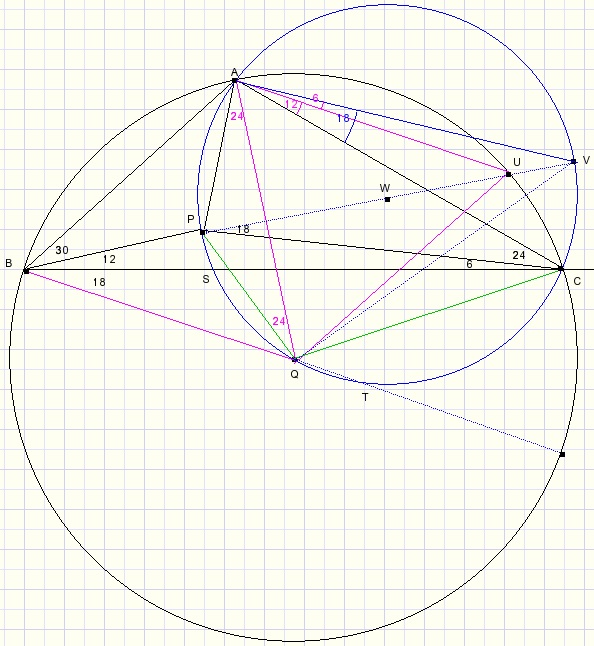
    - LCAU = LPBC = 12 (arc UC = 24)
    - LCAV = LVPC = 18 (arc VC = 36)
    - LVAU = 18 - 12 = 6
    - LPAQ = 24 (arc PQ = 48)
    - LPAV = 24 + 60 + 6 = 90 degrees.


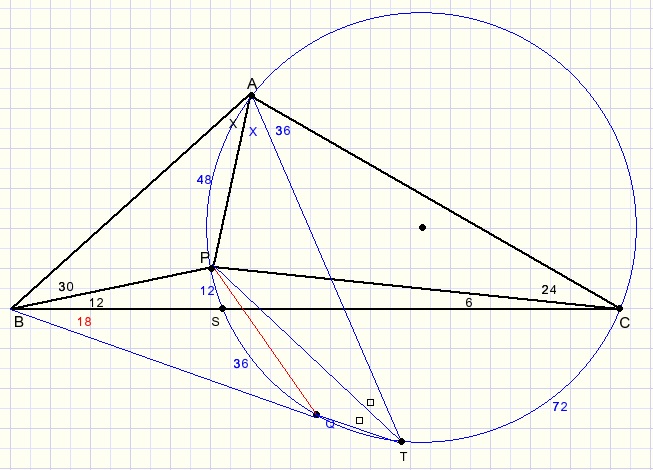
LATP = LPTQ = 24 degrees.
PT is bisector of LT.

LCBT = 18 = (arc CT - arc QS)/2, so arc CT = 72 and LCAT = 36.

The bisectors intersect at 1 point (P) so AP also must be bisector.
LA = 180 - 42 - 30 = 108 degrees.
2x + 36 = 108
x = 36.

Appendix 1

Trigonometric calculation of x:

steps
    1. let AB=1.
    now calculate:
    2. BC with sine rule.
    3. BP with sine rule.
    4. AP with cosine rule.
    5. x with sine rule.



Appendix 2

The theorem of Thales. (Greek mathematician 624 - 547 before Chr.)

Measuring angles with arcs:
definition:
    the size of an arc means: the size of the corresponding angle at the center of the circle.


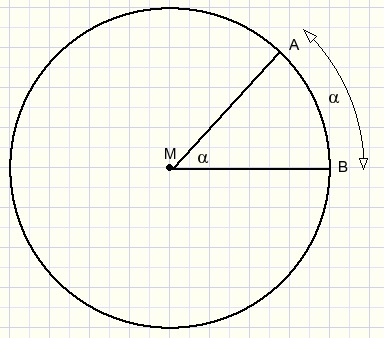
theorem
    an angle on the circumference of a circle is half the size of the arc.


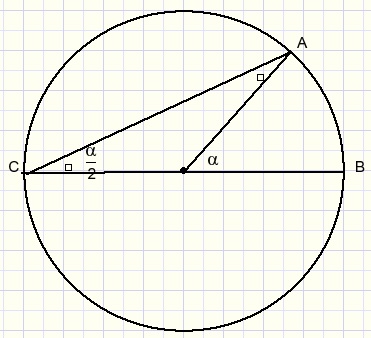
Angle C is half the size of arc AB.
The proof follows from isosceles triangle AMC and the rule that
the exterior angle of a triangle equals the sum of the opposite interior angles.
This theorem is true for all situations, which follows from addition and subtraction of arcs.



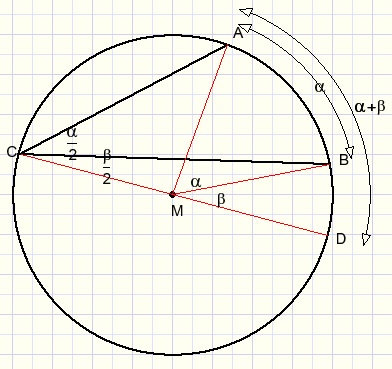
By applying the Thales theorem we can unveil rules for angles inside and outside a circle as well.



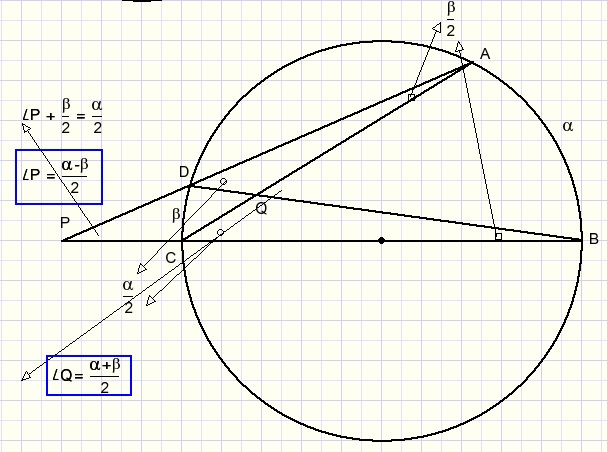
    - an interior angle is equal to half the sum of both arcs.
    - an exterior angle is equal to half the difference of both arcs.
Shown is the easy case where one edge is diameter.
Addition or subtraction of arcs shows that these rules are true for all situations.