Geometry puzzle (16)

Below is pictured rectangle ABCD with BD perpendicular to CE.
Prove that BE x BA = (BC)2.



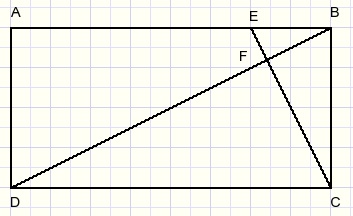
This reminds us at the "power of a point relative to a circle".
First I present some theory.

The power of a point relative to a circle

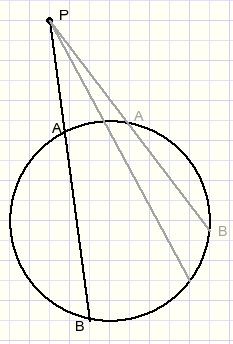
From arbitrary point P outside a circle we draw a line that intersects the circle at points A and B.
Now we notice a remarkable thing:
the product PA x PB is the same for every line.
This product we call "the power op P to the circle".



Proof



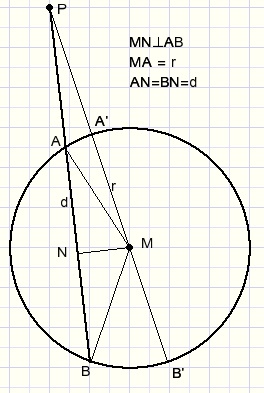
    PA.PB = (PN-d)(PN+d) = PN2 - d2.....1)
    PN2 = PM2 - MN2.....2)
    MN2 = r2 - d2.....3)
    ..2) + ..3) :
    PN2 = PM2 - r2 + d2.....4)
    ..1) + ..4):
    PA.PB = PM2 - r2 + d2 - d2 = PM2 - r2 = (PM-r)(PM+r) = PA' . PB'
Product PA'. PB' is constant.

Solution 1

We notice the circle defined by points A, E and C and the power of B to this circle.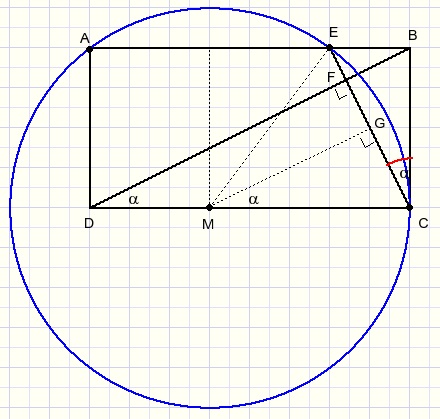



BE.BA = BC2 if BC is tangent to the circle so:
The center of the cirlcle is on line CD.

M is the intersection of the perpendicular bisector of AE with CD.
Draw MG perpendicular to CE.
MG is perpendicular bisector of CE by congruence of triangles MGE and MGC.
M is the intersection of perpendicalar bisectors so is the center of the circle.

The poper of B tot the circle is fixed so: BE.BA = BC2.

Solution 2

This proof uses the properties of similar triangles.
See picture below.