

| Geometry puzzle |
This geometry puzzle is from mr. Omid Motahed, math teacher in Beijing.
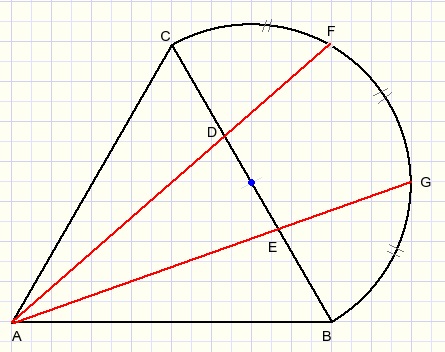
Given are:
Equilateral triangle ABC.
M is the center of BC and also center of a circle arc through B and C.
Arcs CF, FG and GB are equal in length.
Prove that :
CD = DE = EB.
Proof.
Because of the symmetry: CD = EB.
Extend AB and FG, their intersection is H.
Draw lines FM, MG, GB.
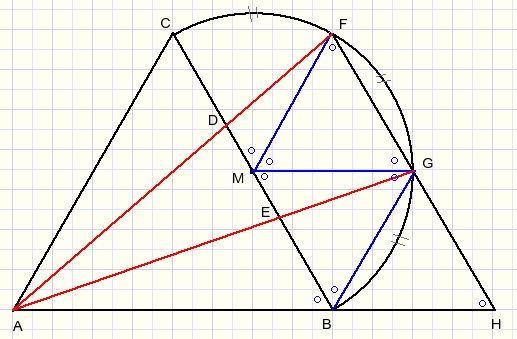
LFMG = 600.....one sixth of 3600
FM = GM, so LMFG = LMGF = 600
Similar:
LGMB=LMGB=LGBM=600.
LBGH=1800-600-600= 600
Conclusion:
FH||BC
Triangles FMG and BMG are equilateral and have a common edge MG.
Triangles BMG and BHG are equilateral and have a common edge BG.
So:
FG = GH.......(1)
Triangles ADE and AFG are similar so:
DE / FG = AE / AG .........(2)
Triangles AEB and AGH are similar so:
EB / GH = AE / AG .........(3)
Combining (2) and (3):
DE / FG = EB / GH now combine with (1):
DE = EB

