

| Geometry puzzle (4) |
This geometry puzzle was brought to my attention by mr. Omid Motahed, math teacher in Beijing.
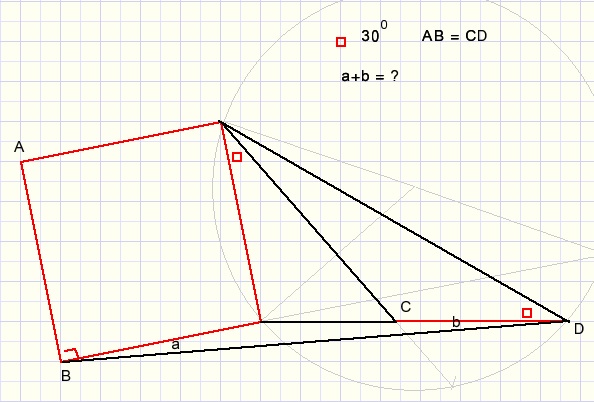
Given is a square and a line CD = AB.
Some angles (indicated by a small red square) are 300
Asked is the sum of angles a+b.
The first question is how to construct this figure.
The equal angles must span equal circle arcs (Thales lemmas).
So a good start would be to construct a circle through these angles using a radius of AB.
An equilateral triangle is attached to the squares edge opposite AB.
The top angle of this triangle is the center of the circle with radius AB.
The 300 angles span circle arcs of 600, which is part of a regular hexagon
dividing the circle in 6 equal arcs of 600.
Please refer to the grey lines in the picture before.
Asked is the calculation of angles a+b.
Knowing however that the exterior angle of a triangle is equal to the sum
of the opposite interior angles, we may restate the problem as:
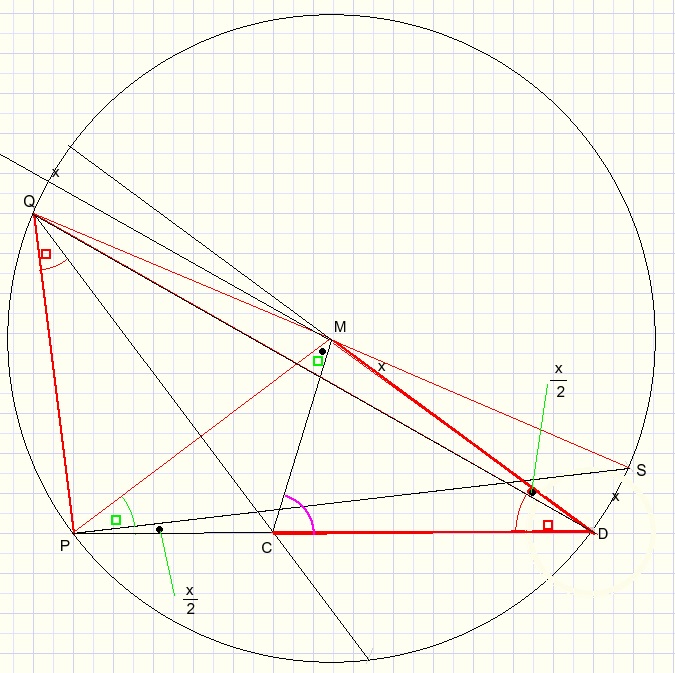
(a+b) = LSPD = x/2 after we call arc DS = x.
Now the problem is how to calculate arc x.
Have a look at LMCD.
This is the exterior angle of triangle PCM and also a base angle of isosceles triangle MCD.
LPQC=300...{given}
LQPS=900...{spans half of circle}
so
LMPS=90-60=300
2.LMCD + LCDM = 1800
LCDQ=300...{given}
Because of isosceles triangle MPC...{C on bisector of MP} :
the following equation emerges:
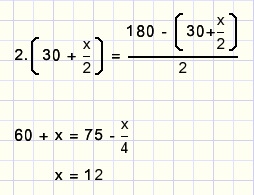
so (a+b) = 60

