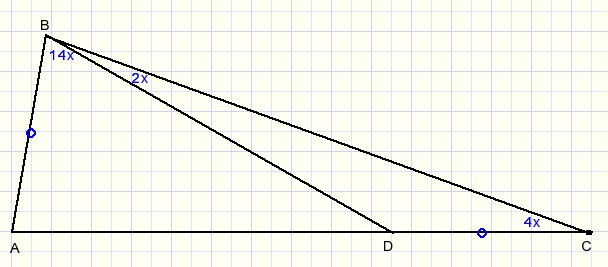
Geometry problem (7) Following geometric problem was found on the Facebook group "Classical Mathematics". Also a picture was provided showing the solution. However, the steps leading to this solution were missing. So the solution shown here is not mine but the steps are. This is the problem: Given are: 1. ΔABC with point D on BC such that AB=DC. 2. The relative size of some angles, see figure (in blue). Asked: find the value of x. 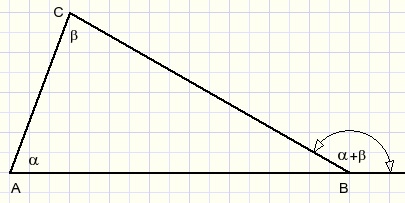During this calculations we apply the lemma: an exterior angle of a triangle is equal to the sum of the two interior opposite angles. Look at the next picture: the calculations Step 1. Draw a circle with center D and radius DC. P is the intersection of the circle with BC, so DP=DC and also LDPC=LPCD=4x. 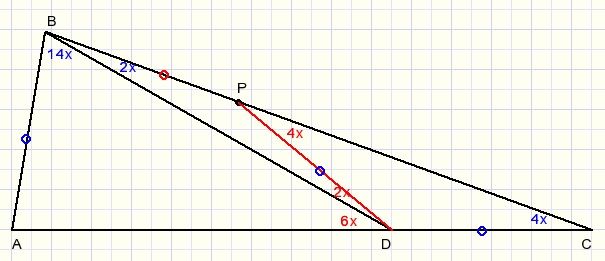LADB=6x ... exterior angle of ΔBCD LADP=8x ... exterior angle of ΔDCP LBDP=8x-6x=2x LPBD=LPDB so BP=DP and also AB=BP (=PD=DC) Step 2. Draw bisector BE of LABC. Point E on AC. 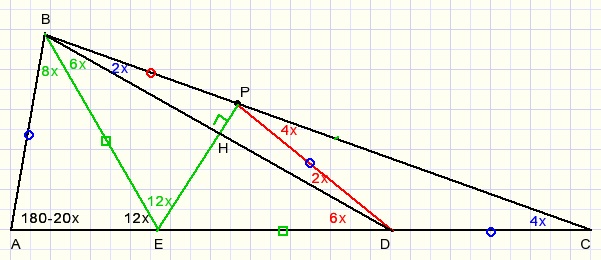LAEB=12x ... exterior angle of ΔBEC LAEB=LPEB=12x ... ΔBEA and ΔBEP are congruent. LEBD=LBDE=6x so EB=ED EP is perpendicular bisector of BD, all angles at point H are 900 Step 3. LBEP=LDEP=12x ... ΔPEB and ΔPED are congruent. Please look at point E: 36x=1800 x=5 A difficult problem.