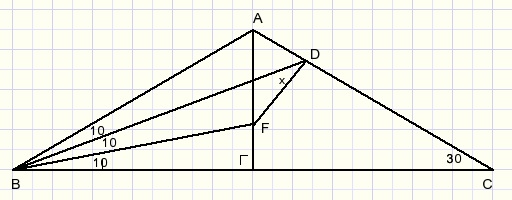
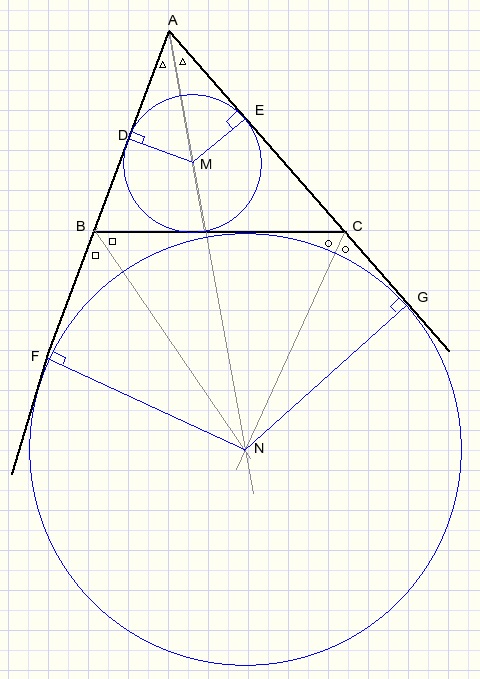
geometry problem (8) Problem: calculate angle x in figure below: A great help is this lemma: the exterior bisectors of two angles of a triangle and the bisector of the third angle intersect at one point. Please look at the picture above: M is the intersection of the bisectors of ΔABC. N is the intersection of the bisectors of exterior angles B and C. M and N are the centers of the inscribed and escribed circles. Lines DM and FN are both perpendicular to AB. LAMD=LANF. So, AN is a straight line. 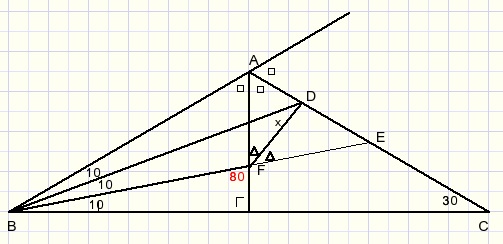The solution 1. extend line BA 2. observe ΔABF 3. BD is interior bisector of B 3. AC is exterior bisector of A 4. D is the intersection of bisectors so, DF is exterior bisector of F 5. LAFE=800 6. LAFD=0,5*80=400 7. x+10 = 40 8. x = 300