Geometry problem solutions 3 (21..29)
21.
This puzzle was found in FaceBook group "geometria":
(by Eldeniz Hesenov)



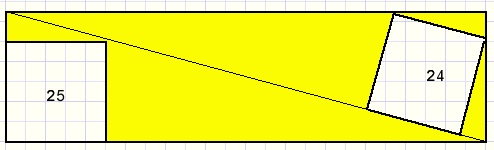
We see a rectangle and within two squares with areas 25 and 24.

Asked: calculate the size of the yellow colored area.

The approach

Best is to calculate the rectangle area then subtract 25 and 24.
Base and height of the reactangle are unknown.
Calling these x and y will need two equations to solve.
However, we notice all similar right angled triangles.
This angles define all other dimensions.
So, as a single variable we choose an angle, see picture.



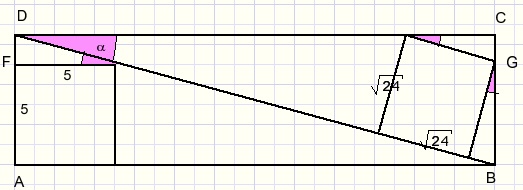
Call this angle α
Given AF=5, AD may be calculated.
Similar BC = BG + GC may be calculated.
At this moment we have two formulas with α which are equal because AD = BC.

Solution




In this equation α has to be solved.
This caused me some troubles, so first I looked for a graphical solution.
In Graphics-Explorer two equations were added:
(x is angle in degrees, y is length)
    formula 1: y = 1 + tan(x)
    formula 2: y = sqrt(24/25)*(sin(x) + 1/cos(x))
At the right top of the Graphics-Explorer screen: selection of degrees, not radians.
Plot the formulas, zoom in to the intersection and read that x = 15.
Unknow at this point is if this answer is correct or just an approximation.

The equation

First we simplify the formula using only the sin and cos functions.
Then the cos(α) denominators are removed.



Now we apply a trick substitution: sin(α)+cos(α)=y

The result is a second degree equation of y.
Below is the proof that this substitution is correct:



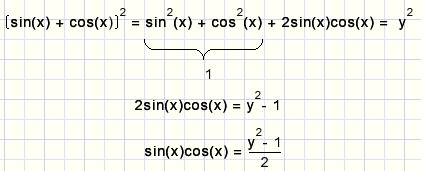
Continuing....
For clarity we temporary write p for the square root of 24/25.
Now apply the ABC rule to solve 2nd degree equations:



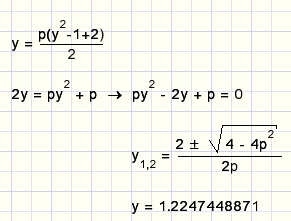
Some standard trigonometric rules are needed:
Please note: cos(30) = y/(2sin(45))



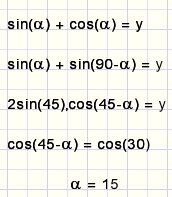
The same answer as we obtained graphical.

The last part:

AD = AF + FD = 5 + 5.tan(15) = 6,34....
AB = 5 + 5/tan(15) = 23,66.....
AB*AD = 150.
The yellow colored area is 150-25-24 = 101.

A very nice problem.
22.
find angle x in the figure below.



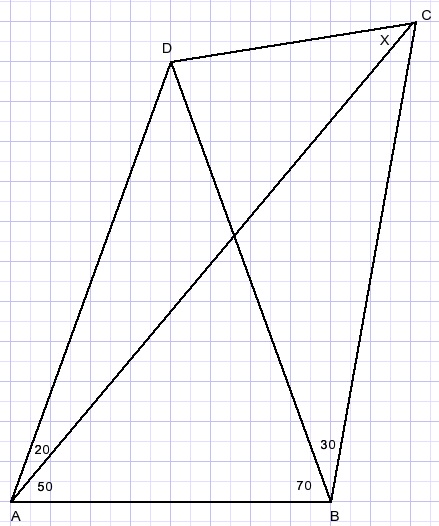
This is not simple, so first we calculate some angles:



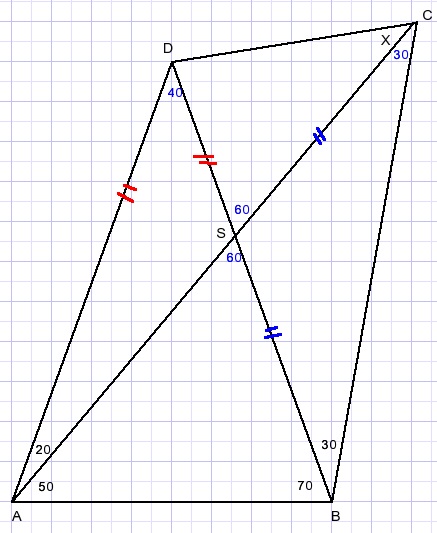
We notice two isosceles triangles: ΔABD and ΔBCS.

Now we apply some intuition.
In the case of isosceles triangles, the top angle is on the perpendicular bisector of the base.
The intersection of two perpendicular bisectors is the center of the circumscribed circle of the triangle.
We construct the circumscribed circle of ΔBCD



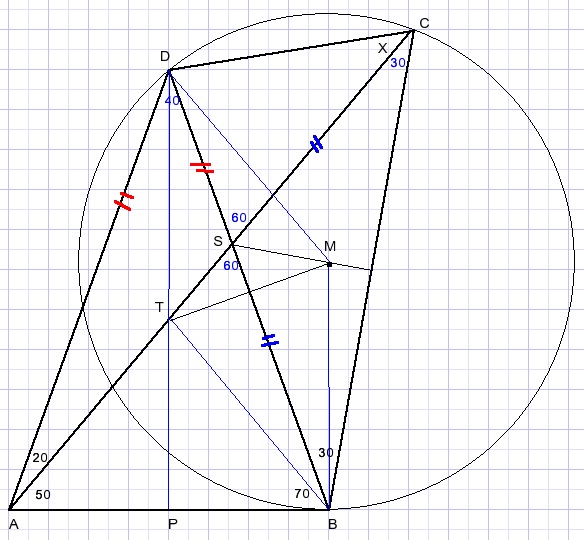
SM is perpendicular bisector of BC.
TM is perpendicular bisector of BD.
DP is perpendicular bisector of AB.
Quadrilateral TBMD is a rhombus because
    MB = MD
    BT = DT
    diagonals BD and MT are perpendicular.
This implies that DT and MB are parallel so LABM = 90.
AB is tangent of the circle.
LABD = LBCD because they span the same circle arc.

x = LACD = 70 - 30 = 40.
23.
Calculate the radius of the small red circle in figure below.



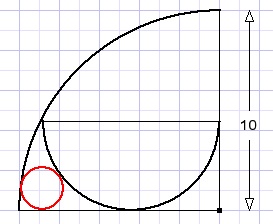
A nice application of the theorem of Pythagoras and the ABC rule (solving Ax2+Bx+C=0)
For clarity the picture is enlarged and lines are added.



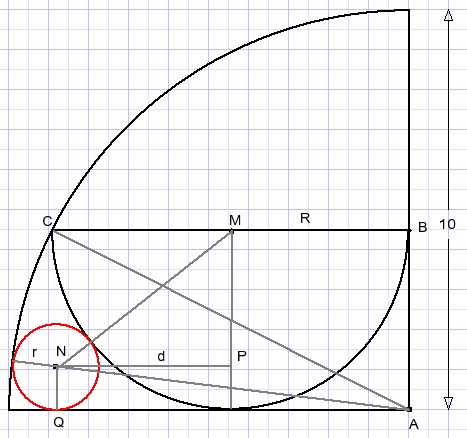
Look at ΔABC and apply the Pythagoras theorem:



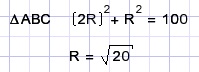
Look at ΔMNP (NP = d) :



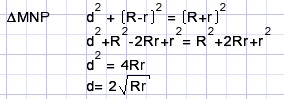
Look at ΔAQN:



Next fill in the values for R and d , simplify:



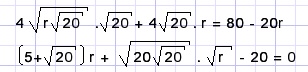
We notice a veiled quadratic equation, just substitute x2 = r.
Application of the ABC rule:



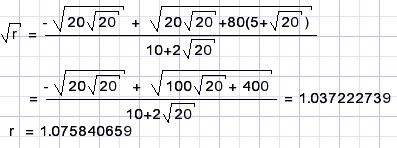
24.
Calculate angle x in picture below.



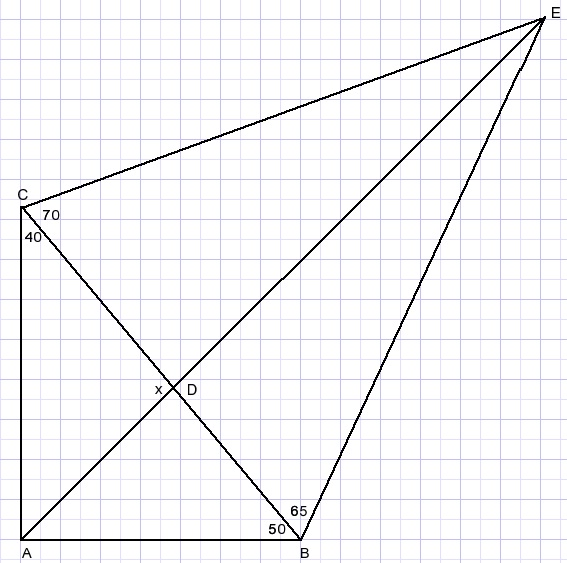
Solution



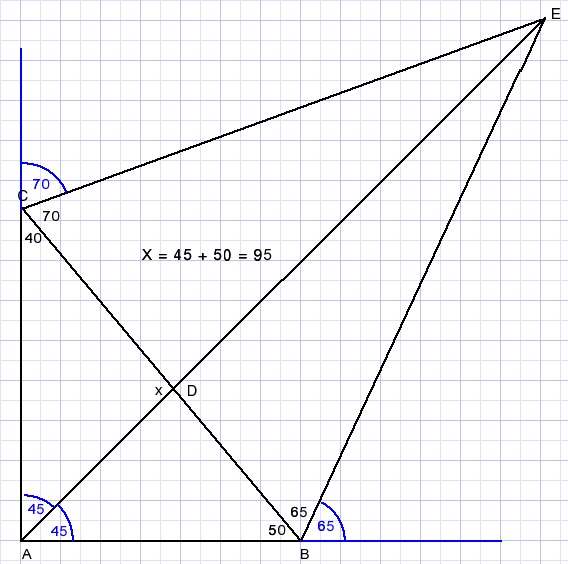
BE and CE are bisectors of exterior angles of ΔABC.
So, AE also is a bisector.
LA = 90
so
LDAB = 45.
x = 45 + 50 = 95.
25.
Calculate angel x in picture below.



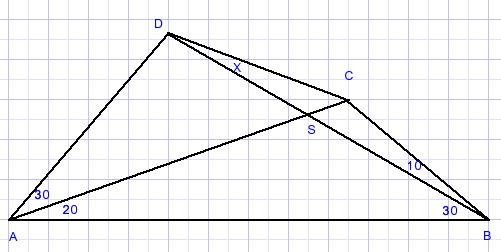
Solution



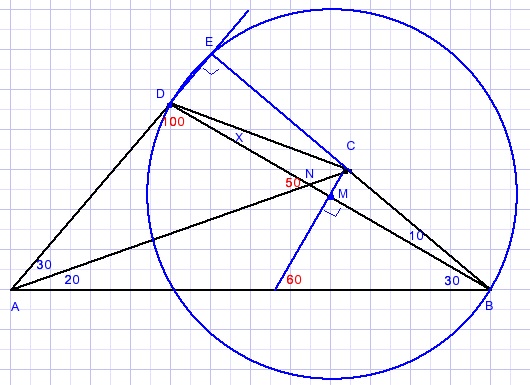
Extend AD and BC, intersection is point E.
ΔABE is right angled.
M is center of circle through DBE. ..{see Thales}
M is center of BD.
Now draw perpendicular bisector of BD.
LMCN = 60 - 20 = 40.
LCNM=LDNA=50.
C is on perpendicular bisector of BD.
BC = DC.
x = L CDB = LCBD = 10.
26.
calculate x in the picture below:



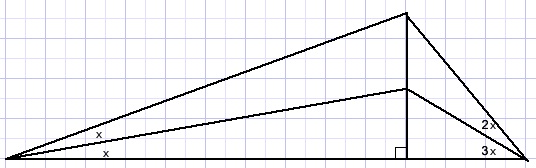
1.Trigonometric approach



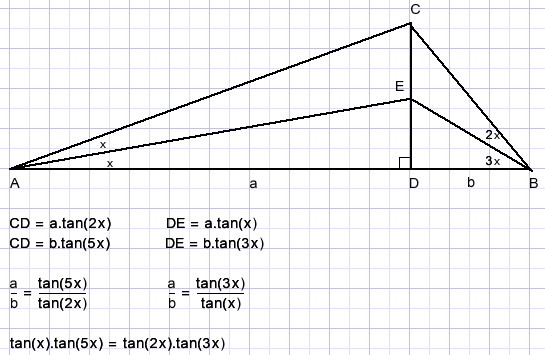
Solving this equation is rather difficult.
Let's make a graph:



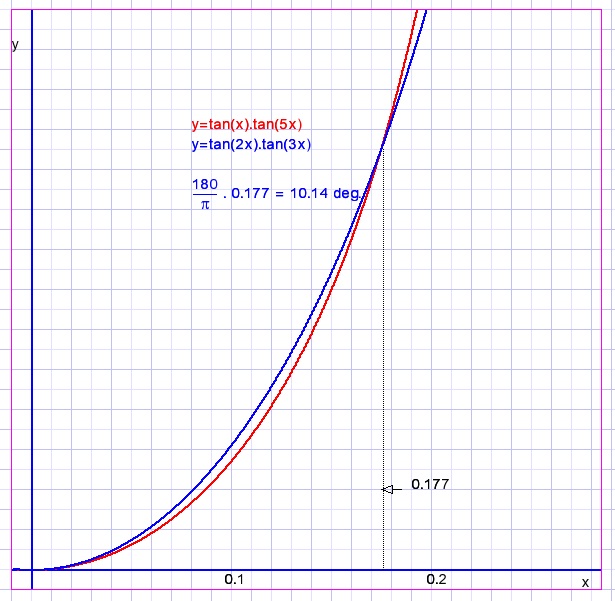
so x is about 10 degrees, most likely exactly 10 degrees.

2.The geometric approach
The 10 degree angle reminds of a regular 36 polygon.
After some experimentation the following picture emerged:



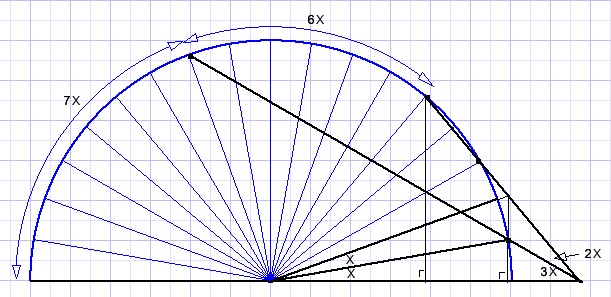
The 7x and 6x arcs are calculated with the Theorem of Thales.

We see:
7x + 6x + 5x = 18x = 180 degrees.
x = 10.
27.
Calculate angle x in the picture below.



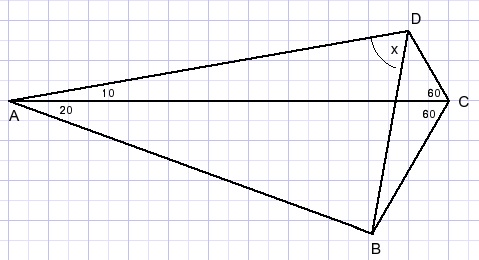
Solution



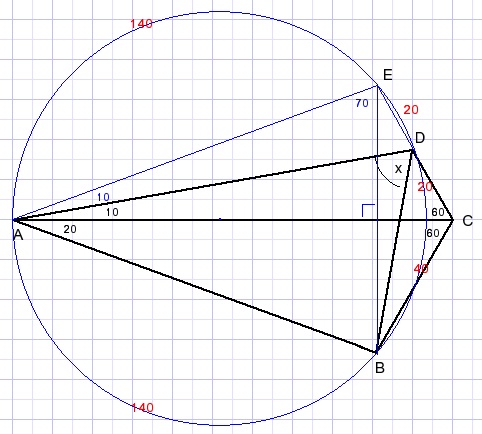
Point E is the reflexion of B over line AC.
Draw the circle through points A,B and E.
LBEA = (180-40)/2=70
Point D positioned on the circle because LACD = (boogAE - 20)/2 = 60 {Thales rules}

x = 140/2 = 70

Note: arc lengths are written red.
28.
Given is quadrilateral ABCD :



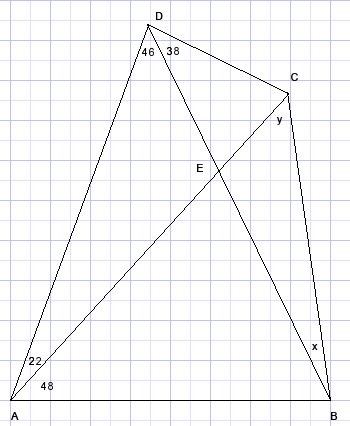
Calculate angles x and y.

Solution

These type of problems can be difficult.
I do not know about a general approach.
Some intuition is required beside trial and error and perseverance.

First we construct the circumscribed circle of triangle BCE.
DC and AB are extended, their intersection is G.
H is the intersection of DG and the circle.



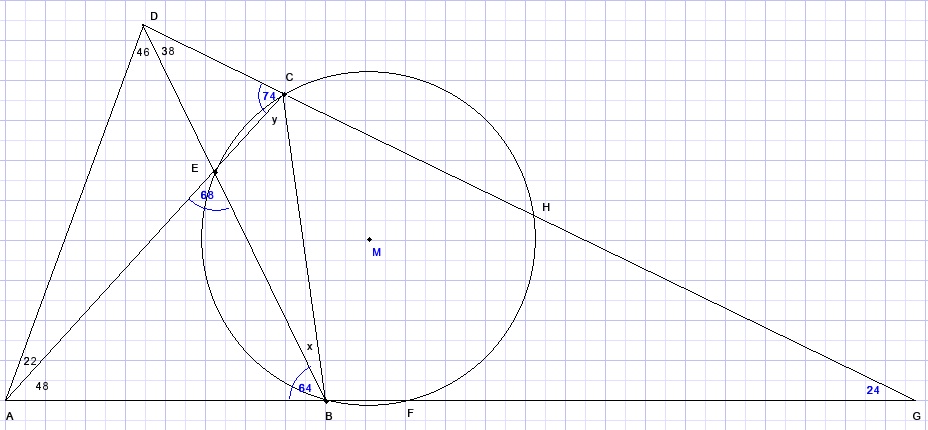
ΔABD....LABD = 64.
ΔACD....LACD = 74.
ΔABE....LAEB = 68

x + y = 68....{exterior angle of ΔBCE}
arcBC = 2x+2y = 136
ΔAGD....LG = 24.
(arcBC - arcFH)/2 = 24
arcFH = 88.

Construct the perpendicular bisector of BC.
This line intersects the circle in H' and the extended line AG in P.



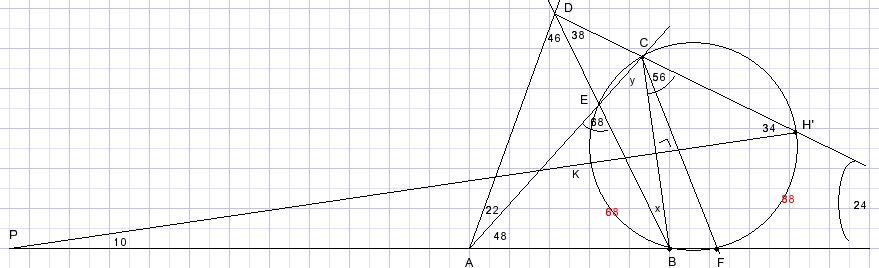
LP = 34 - 24 = 10.
10 = (arcFH'- arcBK)/2.
20 = arcFH' - 68.
arcFH = arcFH' = 88.

Points H and H' coincide.

y = 180 - LACD - 56.
y = 50.
x = 18.
29.
Given



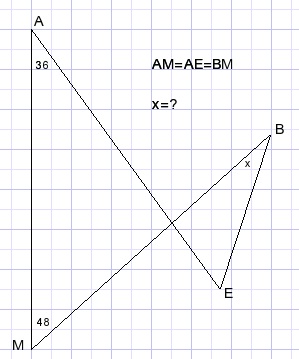
Solution:



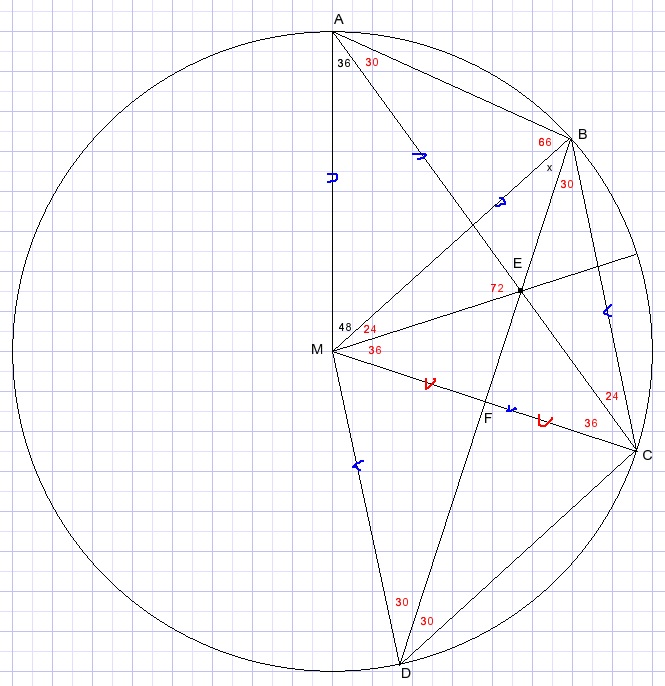
Calculation:
LMBA=(180-48)/2=66
LCAB=66-36=30
boogBC=60
LBMC=60
MB=MC=BC
LAEM=(180-36)/2=72
LBME=72-48=24
LMCA=36
BC=BM en EM=EC : BF is perpendicular bisector of MC
BCDM is a rhombus.
x=LMBF=LDBC=30