the Ultimate Gutter

Luctor et Emergo
(Pump or Drawn)
From the Netherlands, land reclaimed from sea, with it's canals, locks, dikes, ditches
and windmills, a search for the Ultimate Gutter Dimensions..

See section below:
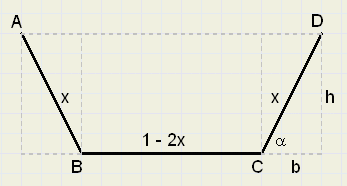In this trapezium the total length AB + BC + CD = 1.

Variables are angle a and length x.

Question: for which values of a and x, will area ABCD have a maximum?

Two solutions are presented:
Dutch windmill
A formula for the area ABCD
See picture above::
The area A is the addition of a rectangle (1-2x)h
and two triangles, together bh, so:
    A = (1 - 2x)h + bh
Note:
    h = x.sin(a)
    b = x.cos(a)
so
    A = x2.sin(a).cos(a) + (1 - 2x).x.sin(a)
    A = x2.sin(a).cos(a) + x.sin(a) - 2x2.sin(a)

the Graphical solution
Graphics-Explorer uses variables x en y.
Also, constants (a,b,c) may be used in formula's.
These constants are changeble by mouseclick, graphics adjust to new values.
It's obvious to use x for a side, y for the area and a for the angle a.

Type the formula:
    y = x^2*sin(a)*cos(a) + x*sin(a) - 2x^2*sin(a)
and change the following settings of Graphics-Explorer:
    - angles: degrees instead of radians
    - coordinates (0,0) left-bottom
    - +/- value for constants increment: 5 (degrees)
    - zoom-center at (0,0)
    - x- scale (1) at right side (x < 1)
    - y- scale (0.2) at top
    - "Autoplot" (to make graphics adjust on constants change)
    - "replace" (to enable cleanup of old graphics)
Plot the formula and change value of a.
Observe maximum value of y and read values of x en a, see picure below:
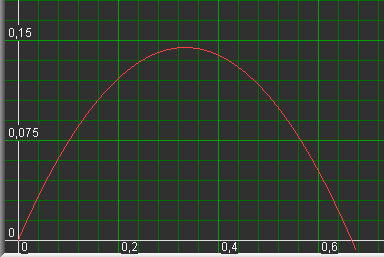While plotting the formula with different values of a, we notice that y has a maximum when the angle
is near 60 degrees and bottom and sides have about equal lengths.

The analytical approach
The maximum or minimum of a function can be found by differentiation.
The derivative of a function equals 0 in this case.
There are 2 variables, x and a,
so, for a maximum of y both the derivatives of A to x as well as A to a must be 0.

Differentiation of A to x
    d A
    d x
     = 2 x ·  sin a ·  cos a +  sin a − 4 x ·  sin a = 0
    2 x ·  cos a + 1 − 4 x = 0
    2 x ·  cos a = 4 x − 1
    cos a = 
    4 x − 1
    2 x
Differentiation of A to a
    d A
    d a
     = x 2 (( cos a) 2 − ( sin a) 2) + x ·  cos a − 2 x 2 ·  cos a = 0
    x 2 ( cos a) 2 − x 2 ( sin a) 2 + x ·  cos a − 2 x 2 ·  cos a = 0
    x ( cos a) 2 − x ( sin a) 2 +  cos a − 2 x ·  cos a = 0
    x ( cos a) 2 − x + x ( cos a) 2 +  cos a − 2 x ·  cos a = 0
    2 x ( cos a) 2 + (1 − 2 x) ·  cos a − x = 0
Now substitute cos(a):
    2 x 
    2
    æ
    4 x − 1
    2 x
    		ö
    ­­
    èø
     + 
    (1 − 2 x) (4 x − 1)
    2 x
     − x = 0
    (4 x − 1) 2 + (1 − 2 x) (4 x − 1) − 2 x 2 = 0
    16 x 2 − 8 x + 1 + 4 x − 1 − 8 x 2 + 2 x − 2 x 2 = 0
    6 x 2 − 2 x = 0
    x = 
    1
    3
Finally, use x to find the best value of a:
     
    cos a
         		 
     = 
     
    4
    3
     − 1
    2
    3
    		 
     = 
         		 
    1
    2

     
So: a = 60 degrees.

The ultimate gutter has sides with an angle of 60 degrees. Bottom and sides have equal lengths.