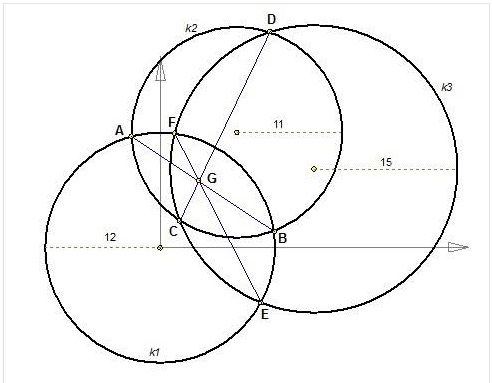
the intersecting chords problem Next I present a geometrical problem which was published on Facebook by mr. Omid Motahed. Three circles intersect each other at two points. The three common cords AB, CD, EF appear to intersect at one point G. The problem is: "why one point"? This is not easy to prove. However after a twist in thinking, this becomes obvious. To demonstrate this proof I start with a seeming different problem: "how to construct a random pyramid"? 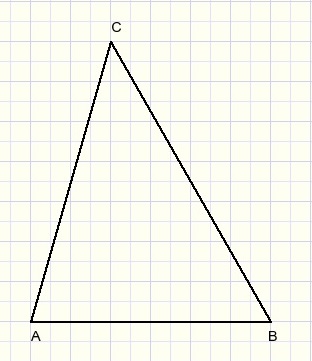First we define a ground plane, ABC: Next we define the projection of the top (T) of the pyramid on the ground plane and we draw lines through T that are perpendicular to AB, BC, AC. 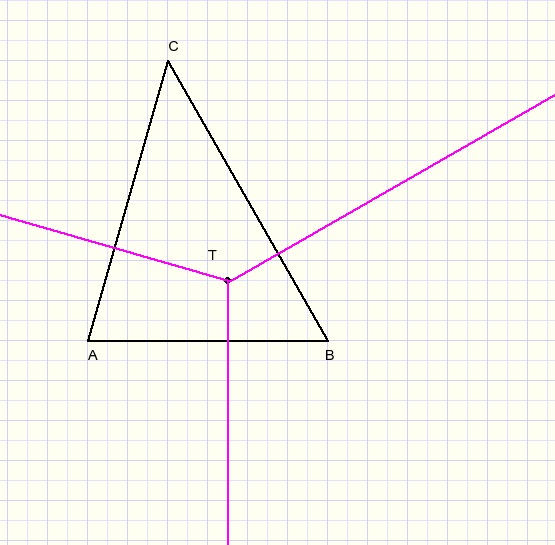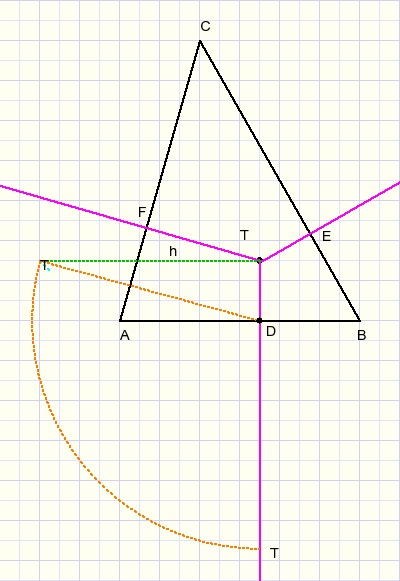Next choose the height of the piramid: say h (h perpendicular to TD), see figure below: Points T are the same, T being located distance h above ground plane ABC. The dotted triangle has to be rotated around line TD until h is perpendicular to plane ABC. Take D as center of a circle with radius TD. Next draw T1A, T1B. Take B as center of circle with radius T1B. Take C as center of circle with radius T2C. Take A as center of circle with radius T3A. 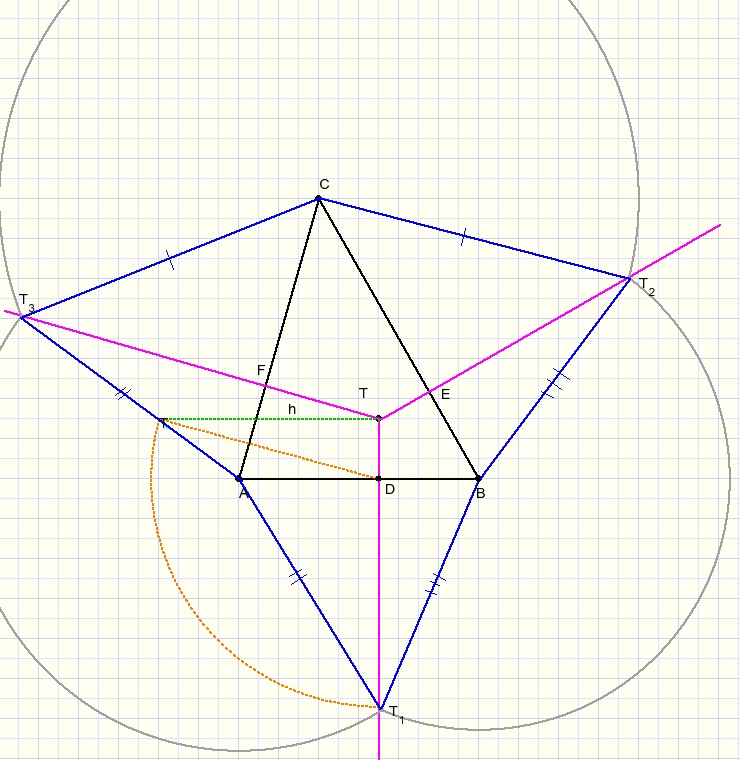So, in above figure we see BT1 = BT2 CT2 = CT3 AT1 = AT3 Now rotate plane ABT1 around AB, rotate BCT2 around BC and rotate ACT3 around AC until points T1 T2 T3 unite. This is pyramid TABC. 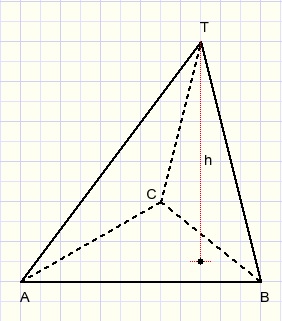Back to the original problem: We paint three intersecting circles with centers A,B,C. Now consider ABC a ground plane just as in the pyramid construction above. 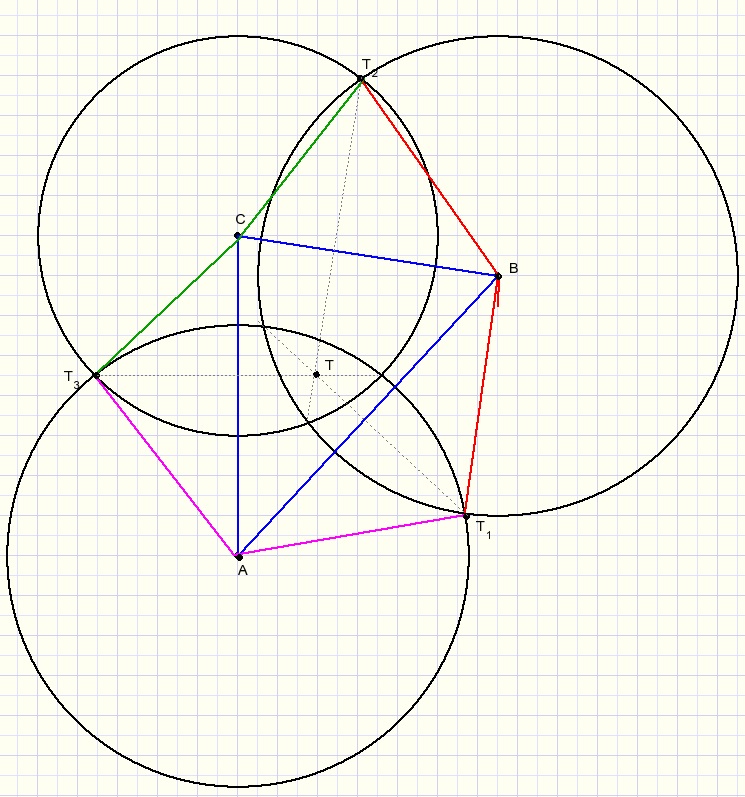Note that the red lines, the green lines and the purple lines are equal in length. So, planes ABT1, BCT2 and ACT3 may be side planes of a pyramid. Now, rotate these planes around AB,BC and AC until the tops T meet. Point G in the original problem is the projection of the top T on ground plane ABC. So, the common chords intersect at one point. Note: if plane ABT1 rotates around line AB, then the projection of T1 on plane ABC moves over the common chord of circles A and B. Etc. This concludes the proof.