Linear Regression

Introduction
In this article I present a nice formula for the regression line though a set of points in a plane.

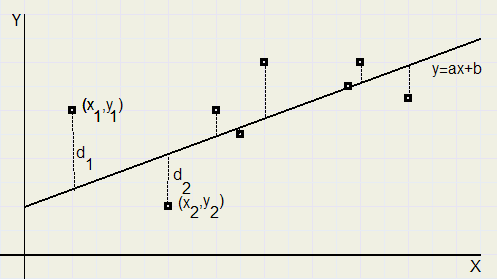
Given are points (xi, yi)...where i = 1,2,...,n
Asked the line y = ax + b which has the least deviation with these points.

A commom measure for the deviation is the sum of squares of the differences:
    d12 + d22 + ..... + dn2
in case of n points.

For point i we have :
    di = yi - (axi + b)
Before continuing, first some definitions and rules:

Definition
    sum:
    S xi = x1+ x2 + .... + xn

    average:
    x
     = 
    Σ xi
    n
Arithmetic rules
    S (xi + yi) = S xi + S yi

    if c is a constant:

    S cxi = c S xi
    and
    S c = n c

    from the average we conclude:
    Σ xi
     = n 
    x
application of the rules:
    Σ
    x
     
    y
     = n 
    x
     
    y
     = 
    y
     
    Σ xi
The formula's for a and b of the regression line y = ax + b
Function f(a,b) of the sum of the squared deviations of points 1..n is:
    f (a , b)
     = 
    Σ (yi − (a xi + b)) 2
f(a,b) is first differentiated to a , then to b.

differentiation to a:
    f 'a(a,b) = 2 
    Σ (yi − (a xi + b)) · −xi
differentiation to b:
    f 'b(a,b) = 2 
    Σ (yi − (a xi + b)) · −1
For the best fit, both derivatives must be zero.
This yields the following system of equations::
    Σ (xi yi − a xi 2 − b xi)
     = 0     ...................1)
    Σ (yi − a xi − b)
     = 0     ....................2)
from ....2) we see
    Σ yi
     − a 
    Σ xi
     − b n = 0
    Σ yi
    n
     − 
    a 
    Σ xi
    n
     − b = 0

    b = 
    y
     − a 
    x
     ................3)
substitute result for b at ........1)
    Σ (xi yi − a xi 2 − (
    y
     − a 
    x
    ) xi)
     = 0
    Σ (xi yi − a xi 2 − 
    y
     xi + a 
    x
     xi)
     = 0
    Σ xi yi
     − a 
    Σ xi 2
     − 
    y
     
    Σ xi
     + a 
    x
     
    Σ xi
     = 0
    Σ xi yi
     − a (
    Σ xi 2
     − 
    x
     
    Σ xi
    ) − 
    y
     
    Σ xi
     = 0
    a (
    Σ xi 2
     − 
    x
     
    Σ xi
    ) = 
    Σ xi yi
     − 
    y
     
    Σ xi
    a = 
    Σ xi yi
     − 
    y
     
    Σ xi
    Σ xi 2
     − 
    x
     
    Σ xi
Formally, we have found the formula's for a and b.
Above value of a can be substituted at .......3) to know b.
However, with some manipulation the formula may be converted into a more elegant form.
We separately attack nominator and denominator.

1. the nominator
    Σ xi yi
     − 
    y
     
    Σ xi
     =
    Σ (xi yi − 
    y
     xi − 
    x
     
    y
     + 
    x
     
    y
    )
     =
    Σ (xi yi − 
    y
     xi − 
    x
     yi + 
    x
     
    y
    )
     =
    Σ (xi − 
    x
    )
     · (yi − 
    y
    )
2. the denominator
    Σ xi 2
     − 
    x
     
    Σ xi
     =
    Σ (xi 2 − 
    x
     xi)
     =
    Σ (xi 2 − 2 
    x
     xi + 
    x
     xi)
     =
    Σ (xi 2 − 2 
    x
     xi + (
    x
    ) 2)
     =
    Σ (xi − 
    x
    ) 2
summarizing:
    a = 
    Σ (xi − 
    x
    )
     · (yi − 
    y
    )
    Σ (xi − 
    x
    ) 2

    b = 
    y
     − a 
    x

Note:
please look [here] for an article about the best polynomial through a set of points.
It is a nice application of linar algebra.