painting 3D Lissajous figures

The lissajous3d program allows the plotting of 3 dimensional Lissajous graphics.
Below is a reduced picture of this (Windows) program at work:
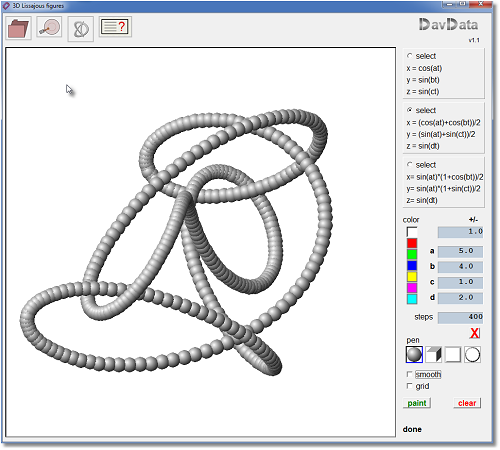
Click at the download (lightning) icon at the top of this page to load the program.

Program features

    - choice of 3 sets of Lissajous formulas
    - choice of 4 pen styles:
      - sphere
      - cube
      - square
      - circle
    - choice out of 7 colors
    - single dots or connected (smooth) lines
    - step count from 100..1000
    - save settings to disc (*.l3d extension attached)
    - load settings from disc
    - save picture (*.bmp)
Selections are made by mouseclicks.
For the constants a,b,c,d :
- a left mouseclick adds the (+/-) value
- a right click subtracts the (+/-) value.
The (+/-) value itself may be changed also by left- or right mouseclicks.

Interim variable t counts from 0 to the selected stepcount.
Stepcount is selectable between 100 and 1000 in steps of 50.

The menu and buttons are self-explanetory.

Below is pictured a "dotted" and the same "smooth" function
    single dots smooth

What are Lissajous functions?

The commonly used functions have the format
    y = ... x ..., where ... stands for operators and constants.
Plotting such a function in a rectangular coordinate system results in a smooth line.
For a given value of x, only one value of y may result.
So, the painting of circles or ellipses is not possible.

This may be overcome by using so called parametric functions, which have the format
    x = ...t...
    y = ...t...
Now, both x and y are a function of interim variable t.

Lissajous functions have the form
    x = cos(...t)
    y = sin(...t)
So, x and y are both periodic functions.
Note: sin and cos are interchangeble.

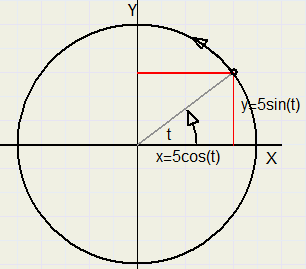
A circle with radius 5 and center at (0,0) is represented by
    x = 5cos(t)
    y = 5sin(t)
Angles are measured in degrees, internal calculations are done in radians where 2p radians = 360 degrees.
360 degrees make a full period.
So, in the picture below, t has to increment from 0 to 360 to paint the complete circle.
More "interesting" pictures may be obtained by adding constants to the functions or use even
addition or multiplication of periodic functions.
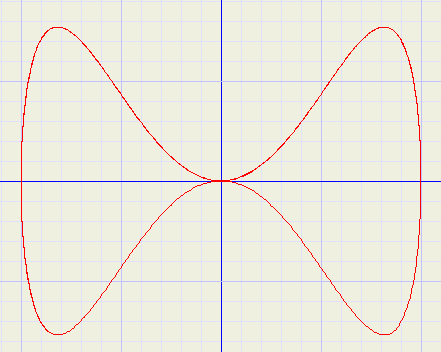x = 2cos(t)
y = sin(t) + sin(3t)

Above picture was made with graphics explorer a functions and equations grapher program.

Lissajous 3D

For 3D, a z axis is added to the X and Y axis.
3D Lissajous functions have the general form
    x = cos(..t)...
    y = sin(..t)...
    z = sin(..t)...
Note: sin and cos functions are interchangeble.
The picture at the top of this page represents
    x = 0.5cos(5t) + 0.5cos(4t)
    y = 0.5sin(5t) + 0.5sin(t)
    z = sin(2t)
Where t runs from 0 to 400.
For each value of t, a sphere is painted.

Additional information

Click [here] for programming information.
This page also has a link to the complete Delphi-7 project source code.
Click on the download (lightning) button at the top of this page to load the Lissajous-3D program.