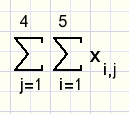| Means, Sum and Product notation |
Constants and Variables
Fixed numbers such as 1 , 2 or 3.89 we call constants.For numbers that are still unknown we write a character such as a, x, or y.
This character is called a variable.
In case of several variables of the same type such as purchases in a supermarket,
we could assign characters a,b,c... for the price of an article.
However more clearly is the use of the same character.
For differentiation a number, called index, is then attached to the character.
A variable with attached index is called an indexed variable.
Three indexed variables x are x1, x2, x3 ....
De Sum notation
The sum x1 + x2 + x3 is written as: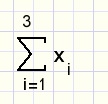
i is the index, it's values are subsequently 1,2,3.
Below the sigma character is the index and it's start value,
above the sigma the end value of the index is written.
Two more examples of sum notations:
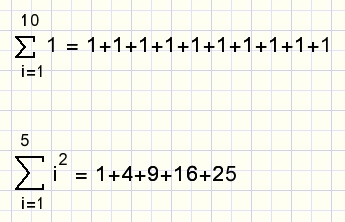
The Product notation
There is a similar notation for the product of numbers:x1 . x2 . x3 is written as:
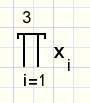
Arithmetic mean
The arithmetic mean is obtained by adding the numbers first and then dividing the sum by the number count.
Example:
We buy Christmas presents of €12, €9, €22, €40 and €17.
Total costs are €100 for 5 items.
So, the average (mean) price was 100/5 = €20.
Sum notation of the arithmetic average of n numbers:
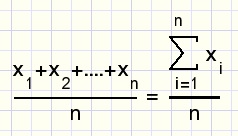
Geometric mean
The geometric mean is obtained by multiplying the numers and then calculate the n'th root of the product.
Example:
A person owns shares and has annual profit margins of 3%, 5%, 10% and 7% .
The average profit is the 4th root of the product 1.03 * 1.05 * 1.1 * 1.07 = 1,062 which is 6.2%.
Product notation for geometric mean of n numbers:
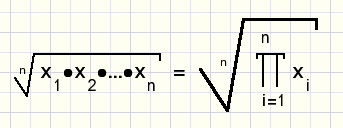
Harmonic mean
Example:
A bath tub has two taps.
Tap 1 fills the tub in 15 minutes.
Tap 2 fills the tub in 9 minutes.
What is the average of these taps?
After opening of tap1 for 1 minute the tub is filled for 1/15th.
For tap 2 this will be for 1/9th. Together the taps fill the tub for 1/15 + 1/9 per minute,
so the tub will be full after 1/(1/15 + 1/9) = 5.625 minutes.
Two equal taps each filling the tub in 2*5,625 = 11.25 minutes had accomplished the same.
Example:
A car drives a distance speeding 100km/hour then turns and drives back at 70km/hour.
What is the average speed?
Of course this speed is: total distance / total time.
Say, the distance is 1(km).
The distance is driven in 1/100 hours, the way back takes 1/70 hours.
The average speed is: 2/(1/100 + 1/70) = 82.35km/hour.
The harmonic mean of n numbers:
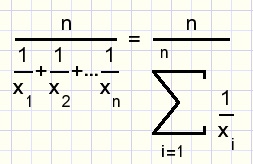
Weighted means
Class 1a counts 30 students and class 1b has 20 students.Class 1a mean score for a math exam is 6.
The mean score for class 1b is 7.2 .
What is the average score per student in classes 1a and 1b?
This is 30*6 + 20*7,2 and dividing by 30+20 results in 6.48 .
The numbers 30 and 20 we call weight factors
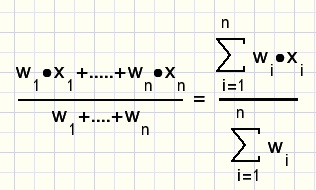
The weighted arithmetic mean of numbers x1..xn with
weight factors w1..wn is:
The denominator being 1 simplifies the formula.
Example:
A final rating is obtained by a paper, written test and an exam.
Weight factors are 0.2 0.3 and 0.5.
A student has rating 9 for a paper, 4 for a written test and 6 for an exam.
The final rating is 0.2*9 + 0.3*4 + 0.5*6 = 6
Pitfalls
Most averages are arithmetic. This involves adding of the numbers.So, if the numbers apply to a situation where addition is not possible, this mean value is meaningless.
Example:
Say on average we receive 3 liters of water daily, which is sufficient.
However for one week per year there is no water at all.
Without the possibility to store (add) water we will not survive.
Windmills face a similar problem because there is no (large scale) storage of electricity.
On average wind blows sufficiently only 30% of the time.
This number is totally misleading: no wind means no power.
Sum of Sums
Below is pictured a two dimensional table of 4 rows and 5 columns.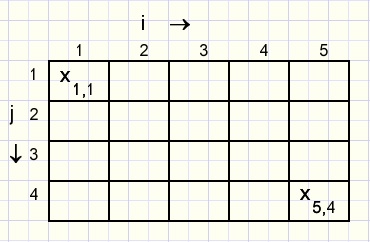
Each field holds a number x.
The x in column 5 and row 4 is written x5,4.
To add all numbers in the table we first sum rows, then add the sums.
The sum notation becomes: