| A mechanics problem |
Introduction
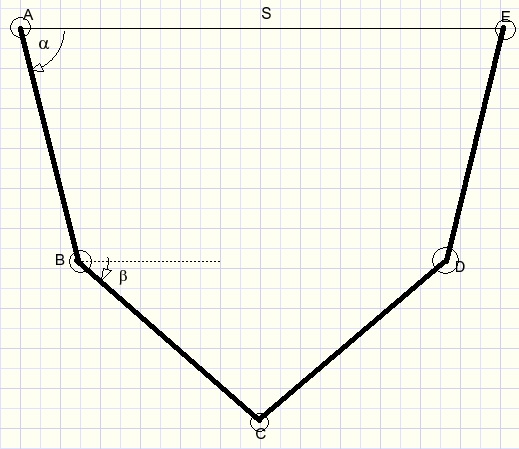
Four identical rods are connected in the above picture.
Rotation is possible around points A,B,C,D,E.
Line AE is horizontal.
A and E cannot move and have a fixed distance S.
Question:
Knowing S and the length of the rods, how to calculate La, Lb and distance BD?
Before we start I present some basics about mechanics.
Representing a force
Forces are painted as lines, the length of the line is proportional to the force.
The force works in the direction of the line.
Adding forces
Forces may be added by building a parallellogram around them.
The sum is the diagonal of the parallellogram:
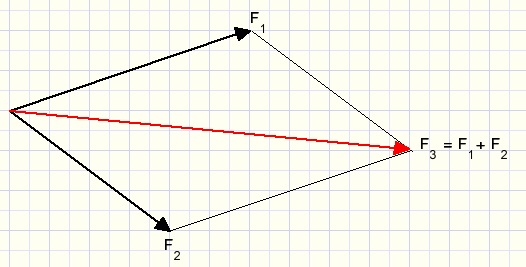
So, applying forces 1 and 2 has the same effect as applying only force 3.
Torque
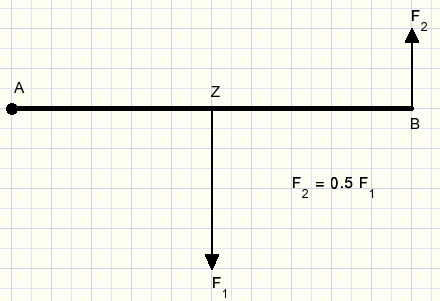
In the picture below rod AB may rotate around point A.
F1 is the force of gravity, which connects to Z, the center of gravity of the rod.
To keep the rod in this horizontal position, we may apply force F2 = F1/2.
The product F2 .AB is called the torque.
An equilibrium exists when the sum of torques equals zero so F1.AZ + F2.AB = 0.
Note: if F1 is positive then F2 is negative because of opposite direction.
Considerations
Please look at the picture at the top of this page.In case of an equilibrium all forces cancel each other.
A is a fixed point.
Forces in the direction of AB are cancelled by an equal but opposite force in A.
A horizontal force in C caused by rods AB,BC will be cancelled by an opposite force from rods CD,DE.
A force BC (right) will cause LABC to stretch towards 180 degrees.
A force CB (left) will cause LABC to sharpen.
Calculations
All forces are the result of gravity.We imagine this force being 1 per rod. (whatever unity
Picture below shows the gravity force for rod AB in it's gravity point Z.
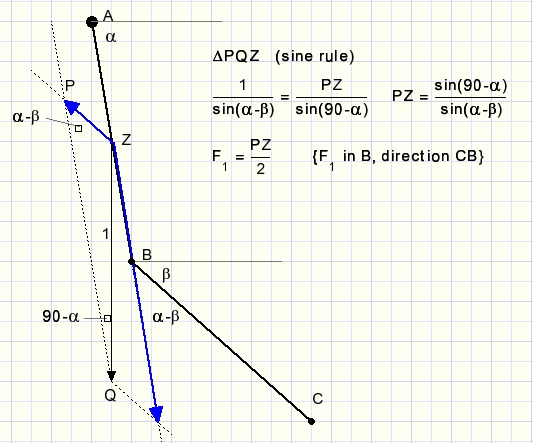
A force ZP in the direction of CB is the result of gravity force ZQ=1.
Force ZP tranferred parallel to point B will be half in value because of the torque rule.
This force we call F1.
Next we observe the effects of gravity forces in rod BC.
First we split this force in values of 0.5 attached to point B and point C.
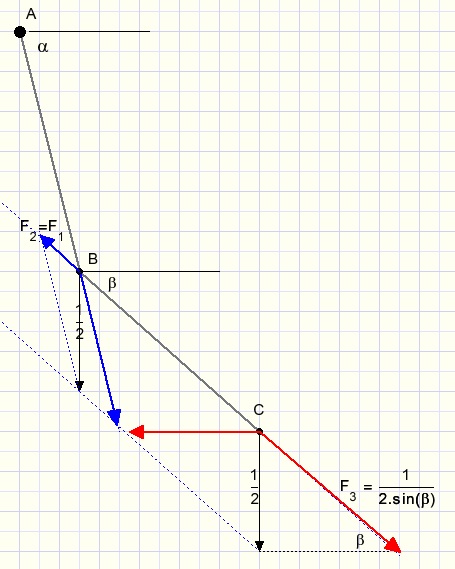
For point B this force results in F2 = F1 direction CB quite similar to the previous calculation.
Now look at point C where gravity force 0.5 is split in force F3 (direction BC)
and a horizontal force which is cancelled by an opposite force from rods CD and DE.
An equilibrium exists when the sum of all forces in point B equals zero.
This is the case if
-
F1 + F2 = F3
or
2.F1 = F3
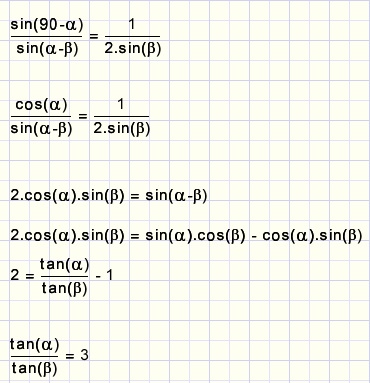
This seems to be the condition for an equilibrium.
Time for verification.

I connected laths of length 96cm with varying distances AE.
For each case I measured distance BD and calculated tan(a) and tan(b).
Surprise !
| AE | BD | tan(a) | tan(b) | |
|---|---|---|---|---|
| 50 | 37.5 | 15.327 | 5.02 | 2.95 |
| 75 | 56 | 10.0557 | 3.279 | 3.07 |
| 100 | 74 | 7.3166 | 2.394 | 3.06 |
| 125 | 91 | 5.5578 | 1.858 | 2.99 |
| 150 | 108 | 4.4607 | 1.469 | 3.04 |
| 175 | 124 | 3.6295 | 1.182 | 3.07 |
| 200 | 138 | 2.93087 | 0.9673 | 3.04 |
| 225 | 150.5 | 2.3753 | 0.792 | 3.00 |
Final question
If the length of a rod equals L and AE = xthis problem starts with the equations:
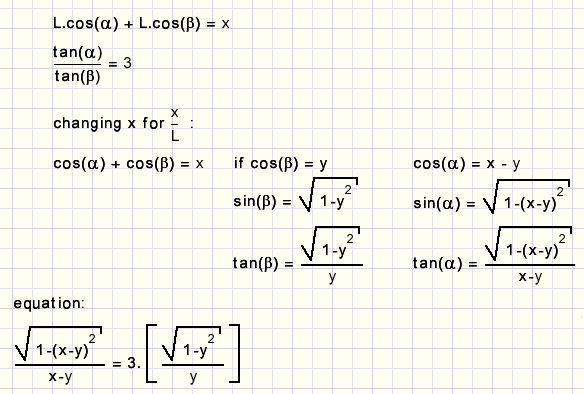
Can this equation be written as y = ....x......?
(I don't think so)
But here is a plot: