distance of parabolas

the distance of two parabolas

The following problem was posted on the Facebook "Matematica group" by Omid Motahed, math teacher in Beying.

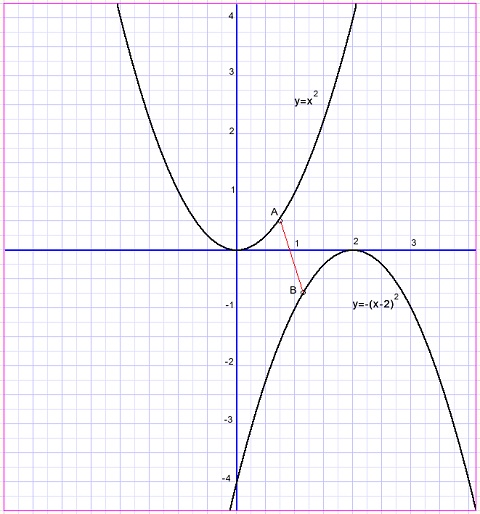
Given are two parabolas.
Find points A and B such that distance AB is minimal.
See figure below:

Two approaches are possible

1. Numerical solution

This was less easy as expected because of the two variable points A and B.
After restarting a few times this algorithm emerged:

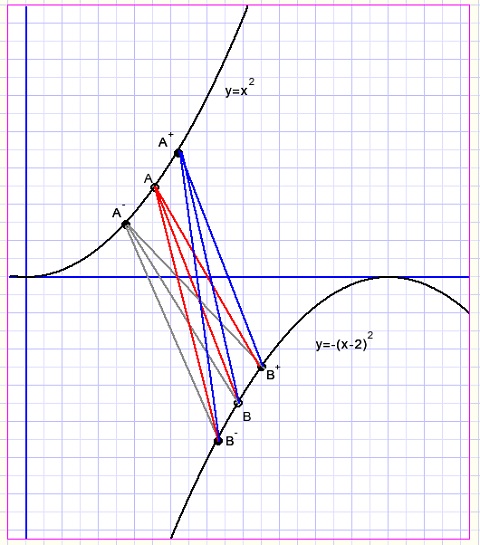
At the start points A and B are choosen and distance AB is calculated.
For A alternate points A⁺ and A^- are positioned at a small step from A.
Similar for B, using the same step.
Now the smallest distance AB^-.....A⁺B⁺ is choosen.
If this distance is smaller than AB, AB is replaced by this distance.
If AB is not replaced, the value of the step is divided by 2.
The procedure repeats until the step value becomes too small.

The Delphi program

 type TDistance = record
                  x1 : single;//A
                  y1 : single;
                  x2 : single;//B
                  y2 : single;
                  D  : single;//squared distance AB
                end;
				
				
var DD : array[0..8] of TDistance;

Array DD contains the coordinates of A(x1,y1) , B(x2,y2) and distance D = AB.
There is one repeat...until loop in which the distances of all 9 connections are calculated.
DD[0] holds AB and is replaced by DD[n] if this has a smaller D value.

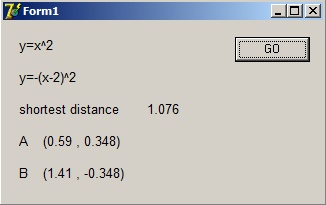
This is the result:

Click [here] to load the complete Delphi-7 project.

Analytical solution

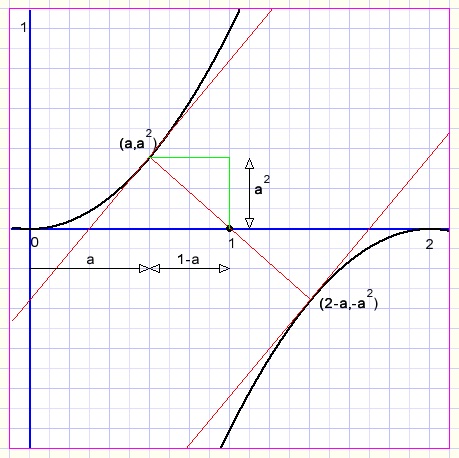
First we choose a point A(a,a²) on parabola y = x².
In this point, the tangent slope will be 2a.
The tangent line of parabola y = -(x-2)² will have the same slope in point B(2-a,-a²)
Line AB crosses point (1,0) for the reason of symmetry.
For being the shortest distance, AB must be perpendicalar to the parabola tangents.
This is true when the product of their slopes equals -1.

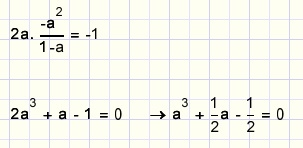
The general solution of a cubic equation as above is:

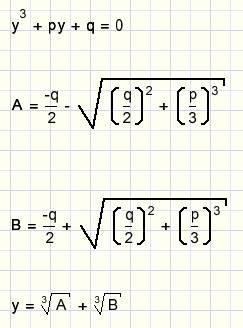
The proof is not part of this article.
For p=0.5 and q=-0.5 we find