partition generator

a partitions generator

download partitions program

download Delphi-7 project

A partition of (integer) number A is a collection of (integer) numbers x_i such that: x₁+x₂+...+x_n = A.

Say we want to know in how many ways a rope of 20cm. long may be cut in 4 pieces.
The sequence is not important so we may sort the pieces from small to large.
All pieces are rounded to the centimeter.

Partitions also show up in puzzle solving where the ages of players add up to a fixed amount
and other constraints have to be satisfied.

This publication presents a short Delphi program that systematically generates partitions.
These partitions are listed together with their rank.
Permutations and combinations may be generated directly from their rank.
For partitions this is not possible.
Rank 3 must be generated from rank 2, rank 2 from rank 1.

To generate partitions we have to know

terms

sum

Here is a list of partitions for SUM = 12 and TERMS = 4
(showing the program at work)

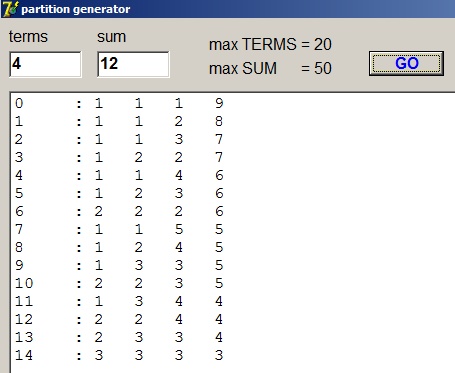
The left column lists the rank.
Terms are sorted small to large.

The partition generating algorithm

Setting the first partition
All columns except the last one are set to "1".
Then the last column is set to SUM - (TERMS-1).

Finding the next partition after 1,1,1,9
please look at picture below:

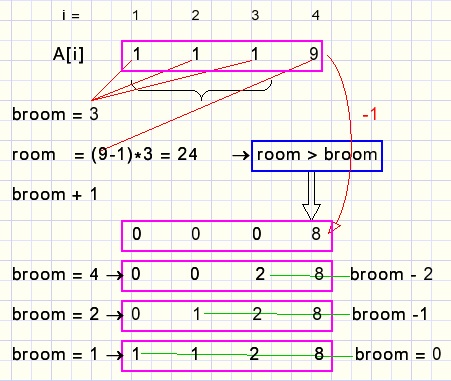
The partition terms are in array A[1...maxTERM].
Index variable i increments 1,2,3,4.
Values A[1],A[2],A[3] are added together in variable broom that sweeps the terms together.
A[4] must be decreased to 8.
Then the terms A[1]..A[3] have to be reset.
This is only possible if these terms may hold the broom.
A[4] being 8 and knowing terms A[1]..A[3] must be <= 8, room = 8*3 = 24 > broom.
The largest value for A[3] = 2, now broom becomes broom - 2 = 2.
The largest value for A[2] = 1, broom becomes broom -1 = 1.
Finally A[1] is set to broom = 1.

This is the general rule:

A next example:
SUM=20, TERMS=5, shown is rank 23 and the calculation of rank 24

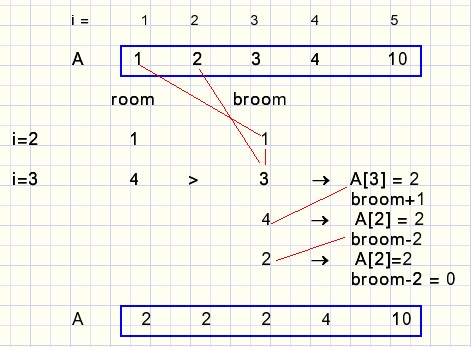
At i=3, room=4 because A[3] may decrement to 2 so the maximum value of A[1],A[2] = 2
room = 2*2 = 4.
broom=3 = A[1] + A[2].
Because room > broom we may decrement A[3] and reset terms A[2], A[1].

Constants and variables:

const maxSUM  = 50;
      maxTERM = 20;

var A : array[1..maxTERM] of byte;
    SUM : byte;
    TERMS : byte;

This procedure sets the first partition (0):

procedure partition1;
//set 1st partition (#0)
var i : byte;
begin
 for i := 1 to TERMS-1 do A[i] := 1;
 A[TERMS] := SUM - (TERMS-1);
end;

And this function calculates the next rank:

function nextpartition : boolean;
//return false if all done
var i,j : byte;
    broom, room : word;
    up : boolean;
begin
 i := 1;
 up := false;
 broom := A[1];
 repeat
  inc(i);
  room := (A[i]-1)*(i-1);
  if room > broom then
   begin
    dec(A[i]);
    inc(broom);
    j := i-1;
    while broom > 0 do
     begin
      if broom-j >= A[j+1] then A[j] := A[j+1]
        else A[j] := broom - (j-1);
      broom := broom - A[j];
      dec(j);
     end;//while
    up := true;
   end
   else broom := broom + A[i];
 until up or (i = TERMS);
 result := up;
end;

If no new partition can be made the function exits with a false result.

For details please refer to the source code.