programming Peg Solitaire

programming Peg-Solitaire

Introduction

Peg Solitaire is a single player puzzle.

The board consists of holes (33) and pegs (initially 32). The center position only is open.
The final, solved, game has one peg in the center position after 31 moves have striked the other pegs.

A move takes a peg over it's neigbour (horizontally or vertically) to an empty hole.
The peg that was jumped over is removed from the game.
See picture below for a reduced image of an initial- and a solved game.


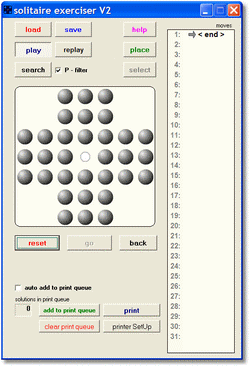initial game	solved game

My version of Peg Solitaire has the following options:

Options

play	search for solutions
replay	replay previous moves or solution
search	have computer search for solutions
place	place balls at board to create starting position for search
select	select 1 of 12 preset games, from easy to difficult
save	save board / solution to disk
reload	reload game from disk
add to print queue	add a solution to the print queue
print	print previously stored solutions
in line help
P - filter	permutation filter removes similar solutions : same moves in different sequence

This article will focus on the search option.

The search algorithm

My efforts to write a program that solves peg-solitaire go back to 1993.
At that time I worked, as a hardware engineer, for the Control Data Corporation (CDC).
I was granted permission to run my Fortran program on the Cyber205, the national supercomputer installed at the Academic Computer Center (SARA) in Amsterdam.
I remember that it took this giant machine about 6 minutes to find the first solution.

Years later I programmed peg-solitair in Pascal.
These programs are lost and recently I wrote another program, now in Delphi.
Also, while camping in France (without PC) some ideas struck me how to speedup the search process.
Peg-Solitaire version 2 is ready now and has these tricks installed. I describe them below.

I know of the existence of search techniques, but never studied them.
My approach is intuitive. Most likely, I have reinvented the wheel.
However, solitaire2.exe solves the solitaire puzzle in 12 milliseconds and finds more solutions in additional fractions of a millisecond.
It is the best result I ever obtained.

Note: the CYBER205 was a 50MHz machine.

A modern PC with 2,4GHz clock needs about 7.5 secs to solve the puzzle
if no addtional tricks are programmed to speedup the search.

Data Structures

Computers can only handle numbers.
How is this game coded? Have a look at the board and the numbering of the peg positions:

The peg placement is recorded in array board:
var board : array[1..49] of byte;

board[n] = 1 if the position n holds a peg, board[n] = 0 if position n is empty.

At this time the reader may wonder why a one-dimensional array is used instead of [1..7,1..7] a two dimensional array.
The reason is speed.
During the search, millions of moves have to be examined.
In the computer memory, bytes are ordered as in a one-dimensional array, so if a two-dimensional array is choosen,
each time a small calculation is necessary to acces the byte. This time is now saved.

From some positions, moves are restricted. (position 3 can only move right or down)
The move directions per position are coded as bits 0..3 in a byte.
A "1" bit indicates that the move is allowed.
See picture below for the coding of move directions:

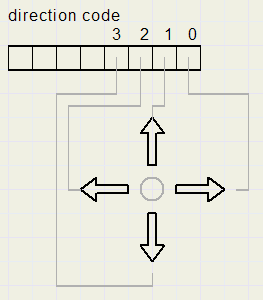
Array movedirs holds the move direction code for each board position.

For positions 1,2,6,7,8,9,13,14,36,37,41,42,43,44,48,49......movedirs[ ] = 0,
so no move from these positions is possible.
See code below

const movedirs : array[1..49] of byte =    //1: right
                 (0, 0, 9, 8,12, 0, 0,     //2: up
                  0, 0, 9, 8,12, 0, 0,     //4: left
                  9, 9,15,15,15,12,12,     //8: down
                  1, 1,15,15,15, 4, 4,
                  3, 3,15,15,15, 6, 6,
                  0, 0, 3, 2, 6, 0, 0,
                  0, 0, 3, 2, 6, 0, 0);

A move is coded as

type Tmove = record
               p1, p2, p3 : byte;
             end;

p1, p2, p3 are board positions (1..49) , meaning: p1 moves over p2 to p3, p2 is removed.
Each move has a number, 1..76 as there are 76 different moves possible.

The pinlist array stores the pins (or pegs) involved in that move.

var pinlist : array[1..76] of Tmove;

At create time the pinlist[1..76] table is generated from the movedirs[1..49] table.

procedure makeMovePinList;
//moves 1..76 translated to pin nrs in PinList[ ]
const u : array[0..3] of shortint = (1,-7,-1,7);  //pin direction increments
var m,n,d : byte;                                 //m:movepin1  d:direction
begin
n := 0;
 for m := 3 to 47 do
  for d := 0 to 3 do
   if movedirs[m] and (1 shl d) <> 0 then
   begin
     inc(n);                //next entry in table
     with PinList[n] do
      begin
       p1 := m;
       p2 := p1 + u[d];
       p3 := p2 + u[d];
      end;
   end;
end;

To avoid confusion, keep in mind the difference between the sequence number of a move and of it's code.
The sequence of moves is, of course, 1,2,3......This is called the move number which has the range 1..31.
The move code has range 1..76 and is used as an index to the pinlist[ ] table to find the pegs involved.

Moves done are stored in table moves[ ]

var moves : array[1..31] of byte;//holds move codes of move 1,2,3... 
    moveNr : byte; //index to the moves table

moveNr always points to the next move in the moves table.

The moves[ ] table shows moves in the format

move number.........................moving pin nr (pin1).....direction arrow

The basic Search Algorithm

A solution is simply a sequence of moves in the moves table.
The complete moves table may be regarded as a 31 digit counter, using the 77th number system.

Then the first number is    0   0   0................................0
The last number is         76  76  76 ..............................76

Regard "76" as a digit and moves[1..31] as a number of 31 digits.
0 means: no move done yet.
70 means: look at pinlist[70] to find pin1, pin2,pin3, the pins involved in the move.

Of course, most combinations of digits are not possible because of wrong peg placement.
Also it is not possible to have two repeating digits like 23, 23.

Counting is very different from the binary, decimal or hexadecimal number systems we are used to.
Starting with 0, 0, 0......(no moves done yet), we test if move(code) 1 is possible.
if so, we perform the move and add the code to the moves[ ] table, which becomes (1, 0, 0, 0..........)
else (the move is not possible) we try move(code) 2, etc......
Say move(code) 5 was the first move possible and moves[ ] becomes (5, 0, 0, .......) and the move number is advanced to 2
and again move(code) 1 is tried. If this move is possible, moves[ ] becomes (5, 1, 0, 0....)
If move76 is tried and the move is not possible, the last move in moves[ ] is taken back and the next move(code) is tried.
example:
Assume moves[ ] = (.................,55, ..........) and no move is possible, so the last move we tried was 76.
Decrementing the move number means pointing to move(code) 55. This move is removed and now move(code) 56 is tried.

This approach also assures that when starting the search at a solved game, the program looks for more solutions,
as the counter is advanced.

In the scheme below, Xmove is the trial move, the one that is investigated.
moveNr points to the next (free) position in the moves table. It is the move sequence number.
Labels are placed in ellipses.
The program uses goto statements to jump to these program positions,
because it has crossing loops which are impossible to program using repeat or while statements.

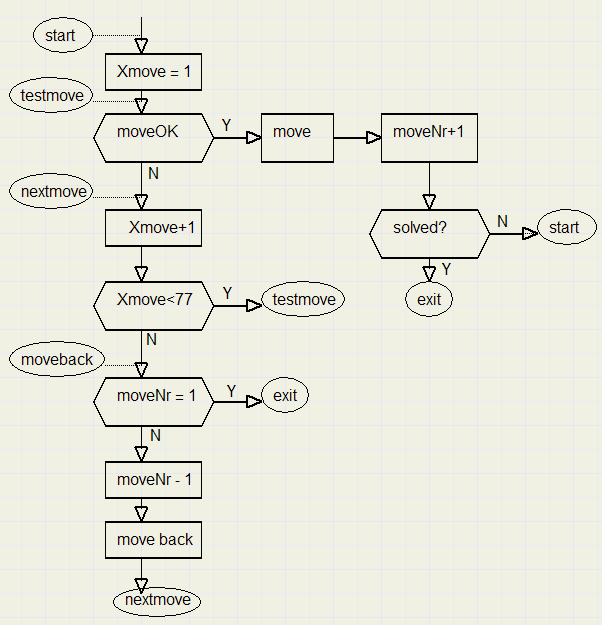
A scheme like this is typical for all so called "brute force" searches.
Brute because of the total absence of intelligence.
Simply all possibilities are tried.
Next, some boxes in the scheme above will be explored in some detail.

The moveOK question box

Here the tests are made to see if Xmove is possible.

testmove :               //test if move is possible

 p1 := pinlist[xmove].p1;
 if board[p1] = 0 then goto nextmove;                      //no pin
 p2 := pinlist[xmove].p2;
 if board[p2] = 0 then goto nextmove;                      //no pin
 p3 := pinlist[xmove].p3;
 if board[p3] = 1 then goto nextmove;                      //no hole

The move box

Here, the move is done

  board[p1] := 0;
  board[p2] := 0;
  board[p3] := 1;
  moves[moveNr] := Xmove;

The solved? question box

  //--- test for solution ----
  inc(moveNr);
  if (moveNr = movelimit) and (board[25] = 1) then
  begin
   result := ssSolved;
   topmoveNr := moveNr-1;
   exit;
  end
  else goto start;

Variable movelimit is 32 for the solitair puzzle. However, some puzzles start with less then 32 pins (or pegs), so the move number
where to test for a solution is puzzle dependent. (But equal to the number of pins the game starts with).

Notice the statement: result := ssSolved.
Search is started by a call to function solve :

function solve : TsearchState;

where:

type TSearchState = (ssTimeout,ssSolved,ssEnd);

ssTimeout means, that the search paused to be continued later.
The timeout code will be introduced later.
ssEnd means that no solution was found.

next move, move back...

nextmove :

   inc(xmove);
   if xmove < 77 then goto testmove;  //move range [1..76]<

moveback :

  if moveNr <= BottomMoveNr then<
    begin
     result := ssEnd;
     topmoveNr := movenr - 1;
     exit;
    end;

   dec(moveNr);                     //point to previous move
   m := moves[moveNr];
   p1 := pinlist[m].p1;
   p2 := pinlist[m].p2;
   p3 := pinlist[m].p3;
   board[p1] := 1;
   board[p2] := 1;
   board[p3] := 0;
   xmove := moves[moveNr];
 end;

   goto nextmove;

Normally, the bottomMoveNr equals 1 and it is the lowest move (number) that can be taken back by the search process.
After manually moving pins to solve a puzzle, the bottommoveNr is incremented to "protect" our own moves.
if at some point the computer is instructed to finish this game, move (numbers) below bottomMoveNr will not be taken back
by the search process. In this way we can configure the board and find out if a solution is possible.
In the moves[ ] table, the move (numbers) below bottomMoveNr are displayed in the color green.

TimeOut
Most games are solved in (much) less then a second.
However, before I added some tricks, the search time was in the order of minutes.
In that case it is convenient to interrupt the search and resume or terminate it.

In the search process, this code was added at the beginning:

begin

 timeout := 100000;      //interrupt timer count
 stopflag := false;

start :                  //(re)start with 1st move

 dec(timeout);
 if timeout = 0 then
  begin
   application.ProcessMessages;
   if stopflag then              //test stop btn was pressed
    begin>
     result := ssTimeOut;
     topmoveNr := moveNr - 1;
     exit;
    end
    else timeout := 100000;
  end;

 xmove := 1;             //1st trial move
.....................

Note: topMoveNr is the number of moves stored in the moves[ ] table.
During replay mode, moveNr points to the next move to be performed.

The stopflag is set by pressing the pause button during the search.

By now, the basic idea is explained and it is time to present some tricks to speedup the search.
This all amounts to the avoidance of needless work, by taking advantage of the specific game characteristics.

Pin Differentiation

Look at position 25 on the original puzzle.
A peg (pin) in this position may jump to positions 11, 23, 27, 39 and no place else.
So if, at some point in the search, these positions hold no pin, a solution is not possible.

Also note the corner positions 3, 5, 15, 29, 21, 35, 45, 47.
These pins have to be removed from the corners, which requires a number of specific other pins to accomplish this task.

With this in mind, each position on the board has been assigned a pin type.
See definition below:

      pintype  : array[1..49] of byte =
                 (0, 0, 3, 2, 3, 0, 0,     //1: win
                  0, 0, 2, 1, 2, 0, 0,     //2: win enable
                  3, 2, 3, 2, 3, 2, 3,     //3: corner
                  2, 1, 2, 1, 2, 1, 2,
                  3, 2, 3, 2, 3, 2, 3,
                  0, 0, 2, 1, 2, 0, 0,
                  0, 0, 3, 2, 3, 0, 0);

Note, that a pintype of 2 is required to accomplish the last move.
Also a pintype of 2 is sacrificed to eliminate a pintype of 3 from a corner of the board.
More research may shorten the search, but this is the extra code I added to the moveOK question box:

 
//------- pin differentiation ---

 xp1count := p1count;
 xp2count := p2count;
 xp3count := p3count;

 case pintype[p2] of
  1 : dec(xp1count);
  2 : dec(xp2count);
  3 : dec(xp3count);
 end;//case

 if (xp1count = 0) or (xp2count < xp3count) then goto nextmove;

Note: variables p1count, p2count, p3count are preset at the start of the game and have to be incremented/decremented
during the search process as moves are added or taken back.
xp1count, xp2count, xp3count is used, because the (trial) move may still be rejected for reasons to come.
p1count..p3count is only altered if the move is done.

The P - Filter

Note: P is an abbreviation of "permutation".
The solitair puzzle has hundreds of thousend of solutions.
However, many solutions are almost identical: the same moves but in a slightly different sequence.
Example:
............a.b.......................versus
............b.a......................where a and b are moves.

The P-filter avoids these similar solutions. Not afterward when the solution is found (as did Solitaire version 1)
but already during the search process.
The accelleration is enormous, especially for the more difficult puzzles.

Remember, that moves[ ] is regarded as a 31 digit counter, where a digit is a move(code) ranging from 1 to 76.
Let's assume that somewhere in the search, moves[ ] looks like: {...no idea if this is realistic}

( ....20, 35, 28, 0 .................)

The count (...20, 35, 28,....) is bigger (occurs later in the search) than (...20, 28, 35,.....).
By examining the pin positions of move28 and move35, we may find that some positions coincide, so move35 was needed
to obtain the board state necessary for move28.
However, if the are no coinciding pin positions, then there is no difference between (...20, 35, 28,.....) and (...20, 28, 35,...)
This combination must have occurred earlier in the search, move28 brings nothing new except the same solution
in a little different sequence. Therefore, if moves28 and move35 share no pin positions, move 28 can be skipped
and the next move to investigate is move29.

The above method may be extended to moves that are further apart.
Example: look at this move sequence:

(...40, 50, 55, 70, 16, 0,...............)

If move16 does share pin positions with move40 but does not share pin positions with moves50,55,70,
then move16 may be skipped because there is no difference with the sequence

(...40, 16, 50, 55, 70,...)

which came up earlier already, because is is a lower count.

How to program this tric?
First we need to record which move numbers modify a certain board position.
And because moves are added and taken back during the search, per board position a stack is required.
The top of the stack of a board position indicates the number of the last move that modified this position.
Look at this data structure:

 
var PMStacks : array[1..49,0..30] of byte; //49 stacks of move numbers
    PMHeight : array[1..49] of byte;       //entries per stack

Procedure PMpush adds data to a stack:

 
procedure PMpush(m,nr : byte);
//push nr to stack of board position pins of move code m
var pin,h,i : byte;
begin
 for i := 1 to 3 do
  begin
   case i of
    1 :  pin := pinlist[m].p1;  //get pin1 of move m
    2 :  pin := pinlist[m].p2;  //       2
    3 :  pin := pinlist[m].p3;  //       3
   end;
   h := PMheight[pin] + 1;
   PMstacks[pin,h] := nr;
   PMheight[pin] := h;
  end;
end;

Procedure PMpop extracts data from a stack:

 
procedure PMpop(m : byte);
//remove last entry from stack for pins of move m
var pin,x,i : byte;
begin
 for i := 1 to 3 do
  begin
   case i of
    1 :  pin := pinlist[m].p1; //get pin1 of move m
    2 :  pin := pinlist[m].p2; //       2
    3 :  pin := pinlist[m].p3; //       3
   end;
   dec(PMheight[pin]);
  end;
end;

There is no need to know the data extracted.
The PMpop procedure is called only when a move has been taken back.

Now, if trial move Xmove is investigated and has passed the board[ ] position- and Pin Differentiation tests,
it is interesting to know at which latest move number (1..31) the pin positions of Xmove where modified.
This information is supplied by function lastPmove(..)

 
function lastPmove(m : byte) : byte;
//find latest moveNr that changed pin positions of move m
var pin,x,i : byte;
begin
 result := 0;
 for i := 1 to 3 do
  begin
   case i of
    1 :  pin := pinlist[m].p1;
    2 :  pin := pinlist[m].p2;
    3 :  pin := pinlist[m].p3;
   end;
   x := PMstacks[pin,PMheight[pin]];  //x=latest moveNr modifying p1,p2,p3
   if x <> 0 then
    if x > result then result := x;
  end;
end;

The test (to skip or allow a move) now becomes

 
//------- P filter -------------

 if form1.Pfilter1.Checked then
  begin
   pm := lastPmove(Xmove) + 1;// +1 is the first independent move
   while pm < moveNr do
    begin
     if moves[pm] > Xmove then goto nextmove;//Xmove(code) is smaller,occurred earlier
     inc(pm);
    end;
  end;

This concludes the description of the Peg Solitaire search algorithm.

One more thing is worth mentioning:
Not every solitaire puzzle has solutions.
Some of them can be recognized without actually doing the search.
This is accomplished by assigning a key value to each bord position as below:

  
const  keys : array[1..49] of byte =    //xor of all pins must be 2 =
                 (0, 0, 1, 2, 3, 0, 0,  //middle value
                  0, 0, 2, 3, 1, 0, 0,
                  1, 2, 3, 1, 2, 3, 1,
                  2, 3, 1, 2, 3, 1, 2,
                  3, 1, 2, 3, 1, 2, 3,
                  0, 0, 3, 1, 2, 0, 0,
                  0, 0, 1, 2, 3, 0, 0);

A move always changes 3 pin positions, which have key values 1,2,3.......(not necessarily in this order).
Since board[p1] xor board[p2] xor board[p3] = 0 in all cases, the xor of all key values of the pins does not change
during the search.
The last pin has a key value of 2. So, any start position also should have 2 as the xor off all it's key values,
otherwise no solution is possible.
The test is made by procedure "initsearchmode", which is called when the search mode is selected.

   
procedure initsearchmode;
//called when search mode is selected
//test pin keys for "no solution"
//set movelimit (= last possible move)
var i : byte;
    xrsum : byte;
begin
 moveNr := topmoveNr+1;
 drawmovepointer(moveNr);//places arrow in moves display
 movelimit := GetPincount + topMoveNr;
 clearprintlist;
 xrsum := 2;
 for i := 1 to 49 do
 if board[i] = 1 then xrsum := xrsum xor keys[i];
 if xrsum <> 0 then form1.msgbox.Caption := 'warning: no solution';
end;

Click [here] to go to the Solitaire game page.

Click [here] to load the complete Delphi-7 project.

David Dirkse
solitaire version 2
july, 2010