Pythagorean Triples

Three natural numbers (a,b,c) are called a "Pythagorean triple" if a2 + b2 = c2

Note: calculations using the Pythgoras lemma in most cases result in answers with roots.
The most well-known Pythagorean triple is (3,4,5) because 32 + 42 = 52

Question: are there more triples?

Let's explore
    a2 + b2 = c2
    b2 = c2 - a2
    b2 = (c - a)(c + a)
Now define:
    c - a = x2
    c + a = y2.............so

    b2 = x2y2
    b = xy
next we solve the equations:



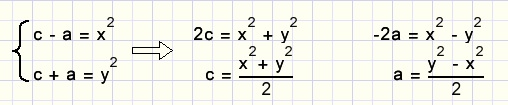
The original formula a2 + b2 = c2 may be rewritten as:



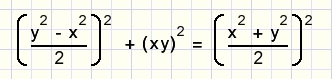
summary:
    a = y 2 − x 2
    b = 2 x y
    c = y 2 + x 2
For each pair of natural numbers (x,y) now a,b en c may be calculated.

Conclusion

There exists an infinite number of Pythagorean triples.

Some triples are not very original as they are just multiples of earlier triples.
Basic triples have no common factors or: GCD(a,b) = 1

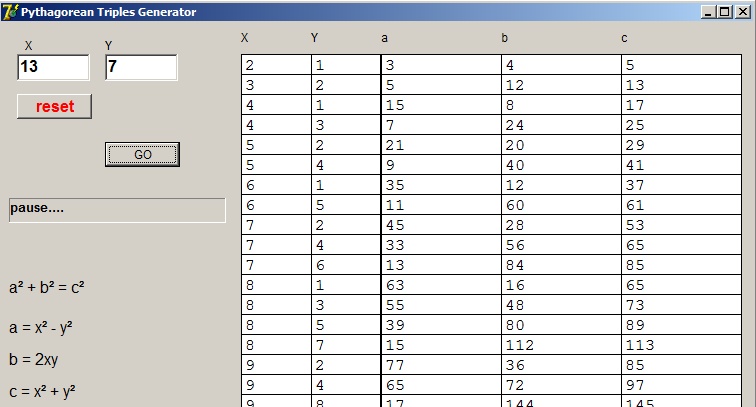
Some results

A small Delphi program calculates the triples:



download program (zip format)
download program (zip format) with angle indication
download Delphi-7 project