Recursive calculation of logarithms

download program.
download Delphi-7 project.

In this article I describe a recursive method to calculate the logarithm of a number.
The programming language is Delphi.

Chained fractions

This is the general format of a chained fraction: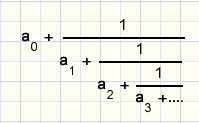



where ai is an integer > 0.
The impact of ai becomes smaller as i increases.
Within a chained fraction the integer part of a number is extracted, leaving a fraction.
The reciproce of this fraction again has an integer part which may be extracted.....
Such a method can be implemented by a recursive procedure.

Logarithms

glog(a) = x means: gx = a
Calculation the logarithm of a number amounts to writing that number as
a base number powered to an exponent and removing the base.

Some rules for logarithms are:
    glog(g) = 1
    glog(an) = n.glog(a)
    glog(a.b) = glog(a) + glog(b)
    alog(b) = glog(b)/glog(a)...and consequently
    alog(b) = 1 / blog(a)
Now we calculate blog(a) and suppose a > b.
(b : base).
a is rewritten as : a = bc.x
where c is a positive integer such that bc < a < bc+1.
The remaining factor x = a/bc < b.
    blog(a) = blog(bc.x)
    =blog(bc) + blog(x)
    =c + blog(x)
    =c + 1 / xlog(b)
and the process repeats itself because b > x.

Recursion

Recursive procedures call themselve.
Because parameters and locally declared variables exist on the stack,
they are unique for each call.
Recursive procedures are very powerfull but also hard to understand.
What helps is to regard them as many different procedures which accomplish the same.

The program

Here is the recursive function: 
function recLog(b,a : double) : double;
//recursive logarithm calculation
//b : base; a : number
var c : byte;
    b2,bt : double;
    GO : boolean;
begin
 c := 0;
 b2 := 1;
 repeat
  bt := b2 * b;
  GO := a >= bt;
  if GO then begin
              inc(c);
              b2 := b2 * b;
             end;
 until GO = false;
 a := a/b2;
 if a > 1.000001 then result := c + 1/reclog(a,b)
  else result := c;
end;
Each step brings a closer to 1 and this makes the test to call the function again.

Variable c is the biggest power of b that fits a.
The successive values of c make the chained fraction.

Please refer to the source code for details of this small Delphi-7 project.