Construction of a Regular Pentagon

Introduction
This article describes the construction of a regular pentagon.
Also explained is why this construction is correct.

The construction
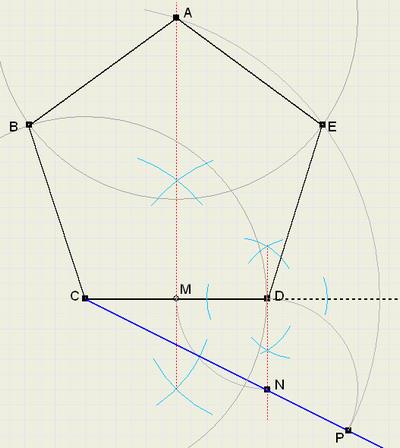
Please look at figure 1.
ABCDE is the pentagon.

    fig. 1

The construction involves the following steps:
    1. choose the length of line CD, the base of the pentagon
    2. construct center M of CD
    3. construct line perpendicular to CD and through D
    4. draw N, so DN = DM
    5. extend line CN
    6. draw circle with center N and radius DN, P is intersection with extended line from 5.
    7. extend perpendicular bisector of CD
    8. draw circle with center C and radius CP, A is intersection with bisector of CD
    9. draw circles with radius CD and centers A, C and D. Points B and E are other angles of pentagon.

Why is this correct?
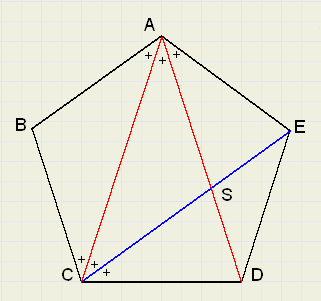
Look at figure 2:
    fig. 2

Each angle of the pentagon is 108 degrees.
    The pentagon may be dissected into 5 equal triangles (with 1 angle in the center)
    All angles of the triangles together are 5 * 180 = 900 degrees.
    Subtract the angles in the center: 900 - 360 = 540 graden.
    Each angle of the pentagon is 540 / 5 = 108 degrees.
Triangle CDE is isosceles, so
LECD = LCED so


Each angle marked + 36 degrees.

CS is bisector of LACD

LCSD = LSDC = 72 degrees, so
    CD = CS = SA
Say the length of CD = 1.

We apply this lemma:
    In a triangle, the bisector of an angle divides the opposite side in parts
    having the same ratio as the sides of the angle
So:
    AC : CD = AS : SD
If AC = x we get :
    x : 1 = 1 : ( x - 1 ) ...........or
    x2 - x - 1 = 0
the ABC rule:
x =
If we can prove that CP = x (see figure 1) than the construction is correct.

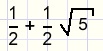Calculation is left to the reader.