Programming Bitmap Rotation
Download the rotation exerciser program
View the source code
Download the complete Delphi-7 project


Introduction

This article describes a Delphi project for bitmap rotation.
There are 3 units:
    - unit1: exerciser to test the rotation procedures
    - rotation_unit : procedures for bitmap rotation
    - clock_unit : time measurement procedures

exerciser

The form has buttons for loading and saving bitmaps.
Also 3 modes of rotation are selectable
    - coarse: fast but less accurate
    - medium: somewhat slower but destination bitmap is fully covered
    - fine: slow, but with soft edges
Bitmaps are displayed in paintbox1.
Moving the mousepointer over the paintbox with leftmousebutton pressed,
causes the picture to rotate in the selected mode.

Below is an example of medium mode rotation
Rotation takes place between a source and a destination bitmap.
In coarse mode, the source bitmap is scanned pixel by pixel and projected on the destination bitmap.
Therefore, not every pixel of the destination bitmap may be covered.
In medium mode, the pixels of the destination bitmap are scanned and their value is loaded
from the source bitmap.
This insures that all pixels of the destination bitmap are covered.
In fine mode, the scanning is the same as in medium mode, but each pixel is divided in 9 equal parts.
Parts may cover different pixels in the source map, the colors are averaged for the final
color of the destination pixel.

Programming

The programmer has to create both the source and the destination bitmap.
Before a rotation may take place, the rotation_unit has to be informed about the names of the bitmaps.
This is done by a call to 
 procedure setmaps(sourcemap,destination map)
Setmaps sets the pixelformat of both bitmaps to 32 bit.
Also, the dimensions of the destination bitmap are adjusted to accomodate
all possible rotations of the source map.

Hereafter, images may be drawn in the source map and 
 procedure coarserotate(deg : word)
 procedure mediumrotate(deg: word)
 procedure finerotate(deg: word)
may be called.
Deg is the rotation angle in degrees from 0..360
Rotation is clockwise, so, for a left rotation of 90 degrees, 270 degrees must be specified.

Do not forget to call the setmaps procedure after loading an image from a file into the source map.
This insures the proper 32 bit format and dimensions of the destination map.

Rotation theory

Medium mode

Picture below shows the coordinate system relative to the bitmaps: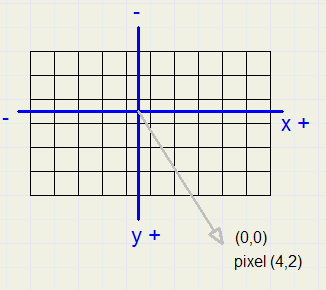
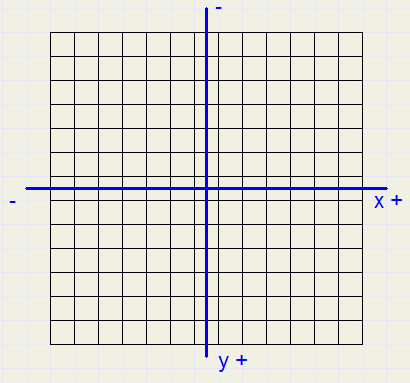    source map destination map
The destination map always is a square.
Also, width and height are odd.
The maps are divided into 4 quadrants
    1 : right bottom
    2 : left bottom
    3 : left top
    4 : right top
Pixel scanning of the destination map takes place from the center outward.
For quadrants 1 and 4, a row is scanned left to right starting at a certain y position.
For quadrants 2 and 3, a row is scanned right to left starting at a y position.

So, for a certain rotated position (x,y) in the coordinate system, the coordinates of the original
position have to be calculated.
Then these positions are used to calculate the corresponding pixels in the source and destination maps.

Let's observe a rotation of 30 degrees (clockwise) using the above bitmaps
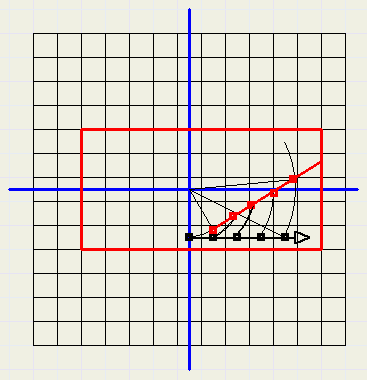    scanning the maps, quadrant 1
The source bitmap is painted in red.
Black pixels of the destination map are scanned, the color is obtained from to corresponding
red pixel of the source map.

Rotation calculation

Now we describe how the position on the source map is calculated given position (x,y) of the destination map.
(x,y) is regarded as the vector addition of (x,0) and (0,y), so the x and the y vectors.
These vectors are rotated separately, then the resulting vectors are added to obtain the rotated (x,y) position.
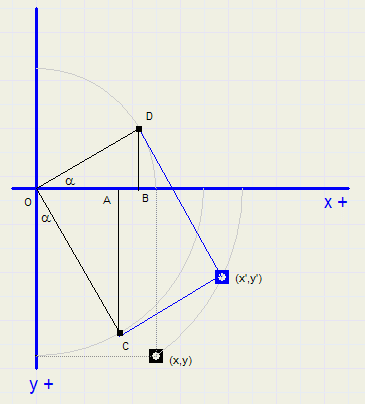
in the above figure, (x',y') is the corresponding source map position which provides
the color for (x,y) on the destination map.

Rotation of the horizontal vector results in OD.
Rotation of the vertical vector results in OC.
OD is the addition of (horizontal) vector OB and (vertical) vector BD.
OC is the addition of (horizontal) vector OA and (vertical) vector AC.

Addition of the horizontal vectors make x', addition of the vertical vectors make y'.

sin( ) and cos( ) functions need the angle in radians.
The call to the rotation procedure supplies the angle in degrees.
Constant deg2rad = p / 180 converts degrees to radians by
    radians := deg2rad * degree
For a rotation angle of a radians and (x,y) as coordinates of the destination pixel:
  • vsin := sin(a)
  • vcos := cos(a)
  • xtx = OB = x * vcos
  • xty = BD = x * vsin
  • ytx = OA = y * vsin
  • yty = AC = y * vcos
xty means : x to y, the contribution of the rotated x vector to the final y vector.

Now, for quadrant 1 :
  • tx = xtx + ytx
  • ty = - xty + yty
For the other quadrants, the signs of xtx, ytx, xty, yty may change.

Addressing the pixels in the bitmaps

Of coarse, Delphi property pixels[x,y] may be used to change pixelvalues.
However, this way is utterly slow.
Also, the scanline[y] property, which returns the memory pointer of the first pixel in row y, is very slow.
Better is to calculate the pointer to a certain pixel.

Because the bitmaps are in 32 bit format we first define 
  type PDW = ^dword;
PDW is a pointer to a 32 bit unsigned variable.

Address calculations are done with variables in dword ( = cardinal) format.
First, the pointer to pixel [0,0] must be obtained.
For this, scanline[0] is used by the setmaps procedure.
scanline[1] returns the pointer to pixel [0,1].
scanline[1] - scanline[0] gives the pointer difference between two rows.

(note: row 1 pointer is smaller then the row 0 pointer).

In the rotation procedure
  • PSBM = scanline[0] for the source map
  • PDBM = scanline[0] for the destination map
  • Slinestep = scanline[0] - scanline[1] for the source map
  • Dlinestep = scanline[0] - scanline[1] for the destination map
Also an adjustment must be made to position the center of a bitmap over (0,0), the coordinate system origin.
  • scx is the center x pixel of the source map
  • scy is the center y pixel of the source map
  • dcxy is the x and y center of the destination map
Now, pixel (x,y) of the source map is addressed by 
    trunctx := trunc(tx);   //tx is floating point format
    truncty := trunc(ty);   //...
    ttx := scx + trunctx;   //add center
    tty := scy + truncty;
    PS := PSBM - tty*Slinestep + (ttx shl 2);   //pointer to source pixel
    pix := PDW(PS)^;
pix receives the color value of the source map pixel.

For quadrant 1, the pointer to the destination map is 
    Ybase1 := PDBM - (dcxy + y)*Dlinestep;
    PD := Ybase1 + ((dcxy+x) shl 2);
    PDW(PD)^ := pix;

Fine Rotation

This is an addition to medium rotation.
Pixel scanning in both modes is the same, however a pixel is subdivided into 9 subpixels:
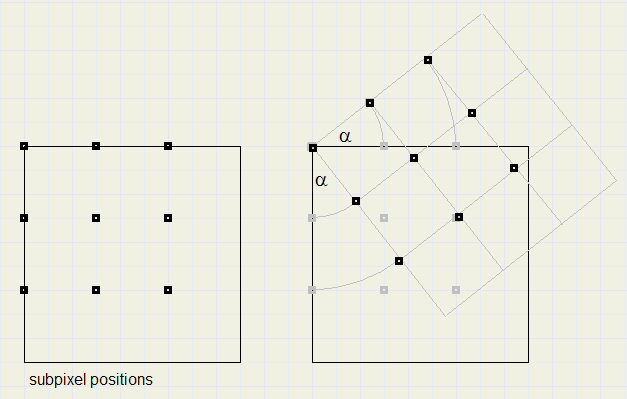At the start of the fineRotate procedure the offset table is generated.
This table is generated for a particular rotation angle and holds the x and y offsets per quadrant
of the subpixel relative to the left top.
For each subpixel position on the source map, the RGB colors are summed.
The final color is the summed color divided by 9.
So, this method is basically nine times slower then the medium mode rotation.

For more details I refer to the source code of the rotation project.
    mediumfine

Donations

This software is free to use.
Programming however is time consuming and hard work.
If you make commercial use of my rotation procedures, therefore consider a donation.
Please contact me for details.