

| ruler and compasses constructions |
This article descibes some basic geometric constructions using only pencil, compasses and ruler.
The ruler enables the drawing of straigth lines, the compasses are for drawing arcs and
for the duplication of equal distances.
Note: the scale of the ruler is not used.
Request: English is not my native language.
In case you discover mistakes in the following article, please inform me.
Also suggestions for improvement are welcome.
Contents
Perpendicular bisector
This is the the most important line in plane geometry.It holds all the points that have equal distance to two other (given) points.
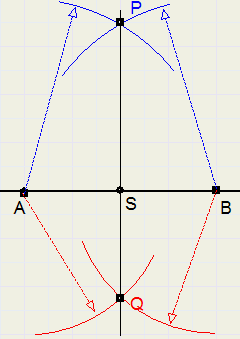
Construct a line perpendicular to AB that intersects AB in the center.
-
1. draw arcs of same radius with centers A en B. Arcs intersect in P
2. again draw arcs of same (other) radius with centers A en B. Arcs now intersect in Q
3. line PQ is the perpendicular bisector of AB
-
S is the intersection of PQ and AB
AS = BS
AP = BP
AQ = BQ
LPAB = LPBA
The circumscribed circle
Given are 3 points: A,B and C.Construct the circle through A, B and C
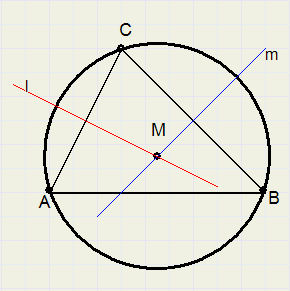
-
1. construct the perpendicalar bisector l of line AC
2. construct the perpendicular bisector m of BC
3. center M of the circle is the intersection of l and m
4. draw circle with center M and radius MA = MB = MC
-
construction of perpendicular bisectors not shown for clarity reasons
The perpendicular bisectors in a triangle intersect at 1 point,
because this point has equal distance (radius) to all three points.
Vertical perpendicular (point to line)
Given are a line l and a point P not on l.Construct a line through P that is perpendicular to l.
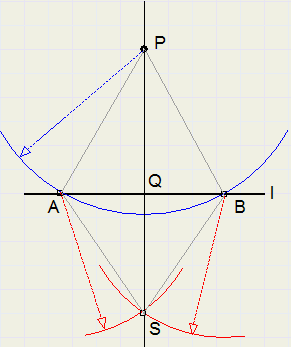
-
1. draw arc with center P, A and B are intersections of arc with l (do not make AB too small)
2. draw arcs with equal radius with centers A en B, intersection of arcs is S
3. PS intersects l in Q
4. PQ is perpendicular to l
-
triangles PAQ and PBQ are congruent , so LPQA = LPQB = 90 degrees.
PQ is the distance of P to l
Vertical perpendicular (line to point)
Given are line lijn l with point P.Construct a line through P and perpendicular to l.
method 1
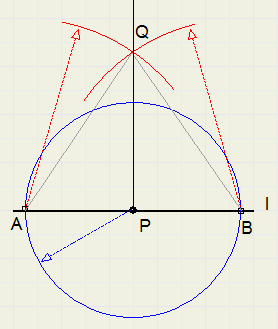
-
1. draw circle with center P, A and B are intersections of circle with l
2. draw arcs of equal radius with centers A and B, intersection of arcs is Q
3. PQ is perpendicular to l
-
LAPQ = LBPQ = 90 degrees, because of congruent triangles APQ and BPQ
method 2
This method applies when P is the end of a line.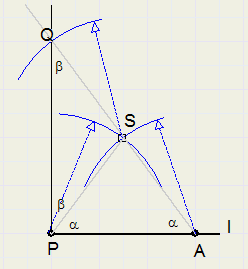
-
1. Choose point A on l. Do not make PA too small.
2. Draw arcs of equal radius with centers A and P, intersection of arcs is S
3. Draw line through A and S
4. Extend AS, draw point Q such that SQ = AS
5. PQ is perpendicular to l
-
triangle APS has PS = AS, so LSPA = LSAP = a
triangle PSQ has PS = SQ, so LQPS = LPQS = b
in triangle APQ 2a + 2b = 180 degrees, so
LAPQ = a + b = 90 degrees
Bisector of an angle
The bisector of an angle splits the angle in two equal parts.Given are lines l and m and their intersection P.
Construct a line n that bisects the angle between l and m.
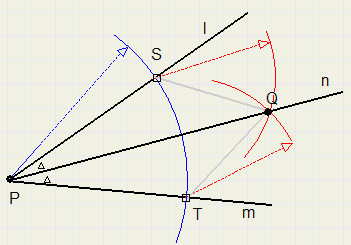
-
1. draw arc with center P, intersections with l and m are S and T. Do not make PS too small.
2. draw arcs with same radius with centers S and T, intersection is Q
3. PQ is the bisector of LP
-
triangles PQS and PQT are congruent, so angles at P are equal.
Each point on n has equal distances to l and m (also because triangles are congruent)
The inscribed circle
Given is triangle ABC.Construct a circle that has AB, BC and AC as tangents.
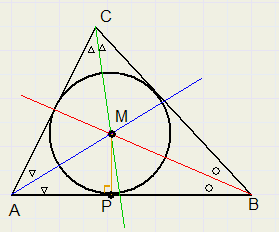
-
1. construct bisector of LA...........(construction not shown)
2. construct bisector of LB...........(same)
3. M is intersection of bisectors and also the center of the inscribed circle.
4. construct line through M and perpendicular to AB.
5. MP is the radius of the inscribed circle.
-
points on the bisector of an angle have equal distance to the edges.
So, M has equal distances to AB, BC and AC
The bisectors of the angles of a triangle intersect in one point.
Parallel line through point
Given are line l and a point P, not on l.Construct a line through P that is parallel to l.
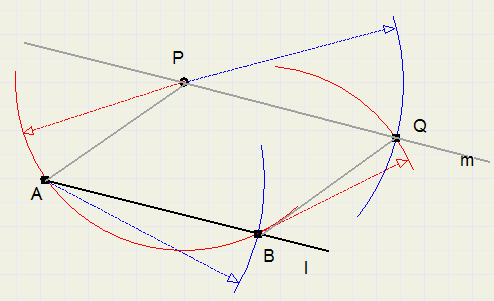
method 1
-
1. draw arc around P, 2 intersections with l (take care that points have some distance)
2. call intersections A and B.
3. draw arc around P with radius AB
4. draw arc around B with radius AP
5. Q is the intersection of arcs ..3) and ..4)
6. PQ is the requested line
-
because PA = QB and AB = PQ, ABQP is a parallellogram.
AB and PQ are therefore parallel lines.
method 2
This is a fast way of parallel shifting.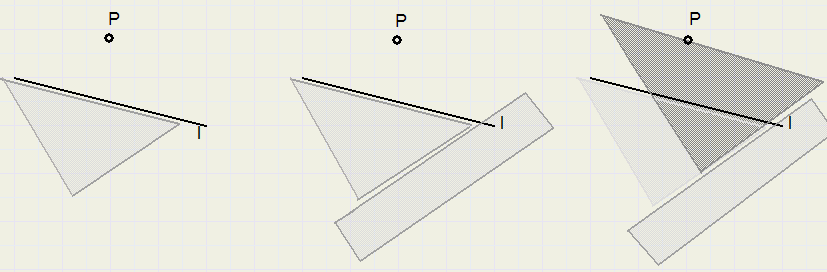
-
1. place triangle along line l
2. place ruler along triangle
3. shift triangle along ruler until P is on edge.
Division of line in equal parts
We divide line AB in five equal parts.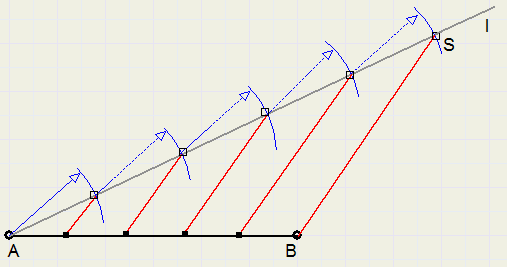
-
1. draw temporary line l through A
2. using compasses, measure 5 equal parts on l, starting at A, ending in point S.
3. draw line BS
4. construct lines parallel to BS, see figure.
5. these parallel lines divide AB in five equal parts.
-
we are using the rule:
"parallel lines divide intersecting lines in parts having the same ratio"
Because all parts on l are equal, parts of AB are also equal.
Tangent of a circle
Given is a circle with center M and a point P outside the circle.Construct a line through P that is tangent of the circle.
method 1
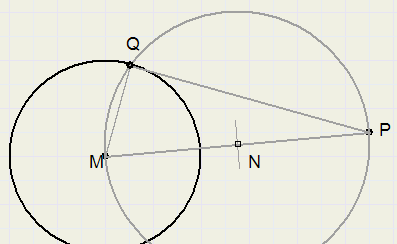
-
1. draw line PM
2. construct point N in center of PM (perpendicular bisector construction)
3. draw circle with center N and radius MN
4. Q is intersection of circles
5. draw tangent PQ
-
LMQP = 90 degrees, because opposite side is diameter of circle N ("Thales rule")
method 2

-
1. draw line through PM. Intersections with circle are U and V
2. adjust compasses to distance UV and draw circle with center M (circle has double length radius)
3. draw arc around P, radius is PM, intersecting big circle in point A.
4. draw line MA, Q is intersection with small circle
4. PQ is the tangent.
-
PQ is perpendicalar bisector of the isosceles triangle PAM,
so PQ is perpendicular to MQ
(the tangent of a circlre is perpendicular to the radius from center to tangent point)
Duplicating an angle
Given are lines l and m, their intersection point A and a point P on line p.Construct line s through P such, that the angle between s and p is equal to the angle at point A.
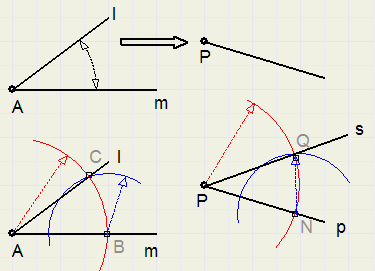
-
1. draw an arc around A. (do not make radius too small) intersection with l is C, intersection with m is B
2. adjust compasses to AB and draw arc around P. (intersection with p is N, see figure)
3. adjust compasses to BC and draw arc around N. Intersection of arcs is Q.
4. draw line s through P and Q
-
triangles ABC and PNQ are congruent, so angles at A and P are equal.
Angles of 30, 45, 60, 72 degrees.
We restrict ourselve to angles of integer degrees.Not every angle may be constructed by compasses and ruler.
It is not possible to construct angles of 1, 2, 4, 5 , 10 ..........degrees.
Only angles being a multiple of 3 are constructable.
In all cases below, given is point A on line l.
Construct a line through A with certain angle to l
30 degrees
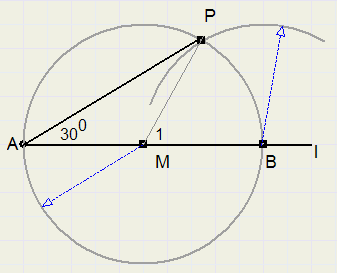
-
1. Choose point M on l, not too close to A
2. draw circle with center M and radius MA
3. circle intersects l also in point B
4. draw arc around B with radius MA, intersection of circles is point P
5. LPAB = 30 degrees
-
triangle MBP is equilateral, so LM1 = 60 degrees.
LA = 30 degrees, because BP is chord of a 60 degree arc. (rule of Thales)
45 degrees
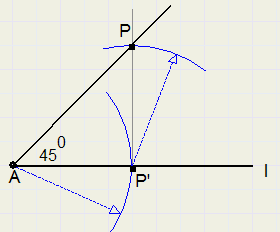
-
1. choose point P', not too close to A
2. construct line through P' and perpendicular to AP'
3. adjust compasses to AP' and draw arc around P', intersection of arc and line is P
4. LPAP' = 45 degrees
-
triangle PAP' is right-angled and isosceles, so other angles are 45 degrees
60 degrees
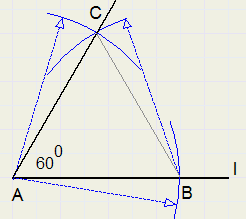
-
1. choose point B on l, not too close to A
2. adjust compasses to AB and draw arcs around A and around B
3. C is intersection of arcs
4. LCAB = 60 degrees
-
triangle ABC is equilateral, so has 60 degree angles.
72 degrees
This construction originates from the construction of a regular pentagon.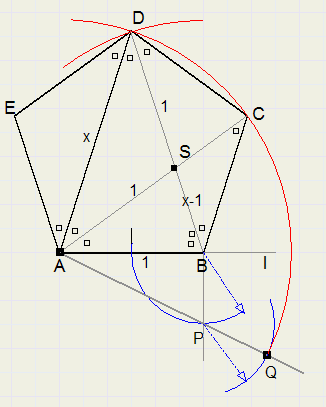
-
1. choose point B on l. (call AB = 1)
2. At B, construct line perpendicular to l
3. construct center of AB
4. make BP = AB/2 .... (BP = 1/2) see figure.
5. draw line AP
6. extend line by 1/2. ( AQ = AP + 1/2)
7. draw arcs around A and B with radius QA, intersection of arcs is D
8. LDAB = 72 degrees.
-
In the figure, equal angles have equal markers. A mark means 36 degrees.
AS is bisector, AB = AS = SD (isosceles triangles)
Let AB = 1 and AD = x. Application of bisector rule:
x : 1 = 1 : (x-1) or:
x2 - x - 1 = 0
x =
| 1 |
| 2 |
| 1 |
| 2 |
| \ | 5 |
Trisection of an angle
Earlier we agreed not to use the scale marks on a ruler.This constraint inhibits this construction.
But if we allow ourselve to add 2 marks to the ruler, the construction becomes possible.
We divide LBAC in three equal angles:
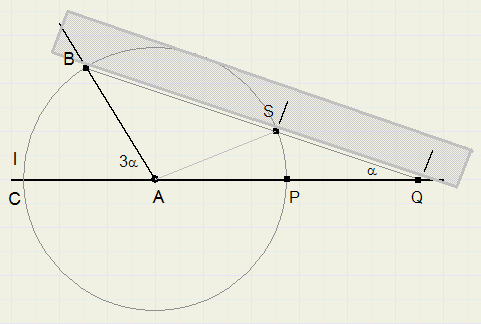
-
1. draw arc around A with radius CA.
2. extend line CA
3. place ruler along CA and draw 2 pencil marks on it, one at point C and one at point A.
4. place ruler along point B and shift until marks are at S and the extension of CA.
5. LBQC = 1/3 * LBAC
-
Let LBAC = 3a and LBQC = x
According to the rule of Thales: x = 1/2 arc BC - 1/2 arc PS = 1/2 (3a - x)
2x = 3a - x
x = a
The square root of a*b
Given are 2 line pieces with lengths a and b.Construct a linepiece with length root(ab).
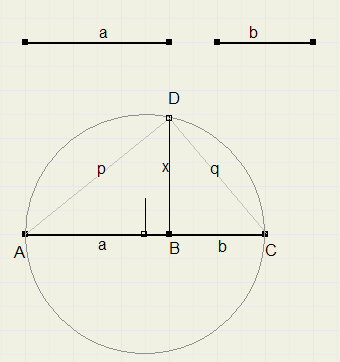
-
1. place lengths AB = a and BC = b together on a line.
2. regard AC as diameter of a circle, draw the circle.
3. construct line perpendicalar to AB, through B.
4. this line intersects circle in D.
5. BD is the right length: root(ab)
-
Let AD = p , CD = q , BD = x
Pythagoras:
a2 + x2 = p2
b2 + x2 = q2
p2 + q2 = (a+b)2
together:
a2 + x2 + b2 + x2 = (a+b)2
a2 + 2x2 + b2 = a2 + 2ab + b2
x2 = ab
Linepiece a * b
Given are linepieces with lengths a and b and also a linepiece of length 1.(without the 1 we cannot know if multiplication makes a linepiece smaller or bigger)
The construction is based on the rule that parallel lines divide intersecting lines in pieces with equal ratios.
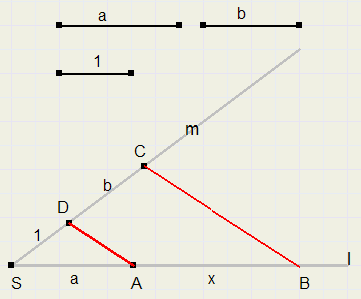
-
1. draw intersecting lines l and m (choose angle somewhere between 45 and 90 degrees)
2. on m, make SD = 1 and DC = b, see figure.
3. on l, make SA = a.
4. draw line AD
5. draw line BC parallel to AD
6. AB = a*b
-
Let AB = x
AD is parallel to BC, so,
SA : SD = AB : DC
a : 1 = x : b
x = ab
Linepiece a / b
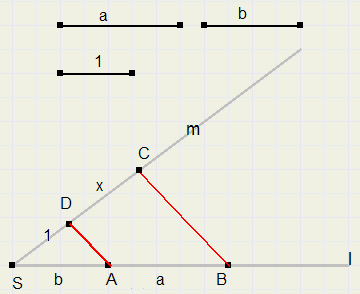
-
1. draw intersecting lines l and m.
2. place distance 1 on m.
3. place distance b (SA) and distance a (AB) on l, see figure
4. draw line AD
5. draw line BC parallel to AD
6. DC = a/b
-
1 : b = x : a
x = a/b
Regular hexagon
Starting with length AB of an edge, we construct a regular hexagon.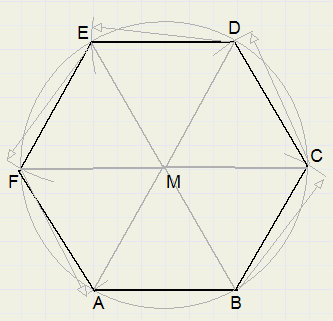
-
1. construct equilateral triangle ABM (draw arcs around A and B, radius AB)
2. draw circle around M, radius MA
3. adjust compasses to length MA, draw arcs around A,B and intersections C, D, E, F
4. draw lines BC, CD, DE, EF, FA
-
all triangles (MAB, MBC ...etc) are equilateral, so all angles are 60 degrees.
So, the 6 angles in the center are 360 degrees together.
Regular polygon with 9 edges.
This construction is only possible by allowing the trisection tric, because angles of 20 or 40 degreesneed to be constructed.
We start the construction from the length of edge AB.
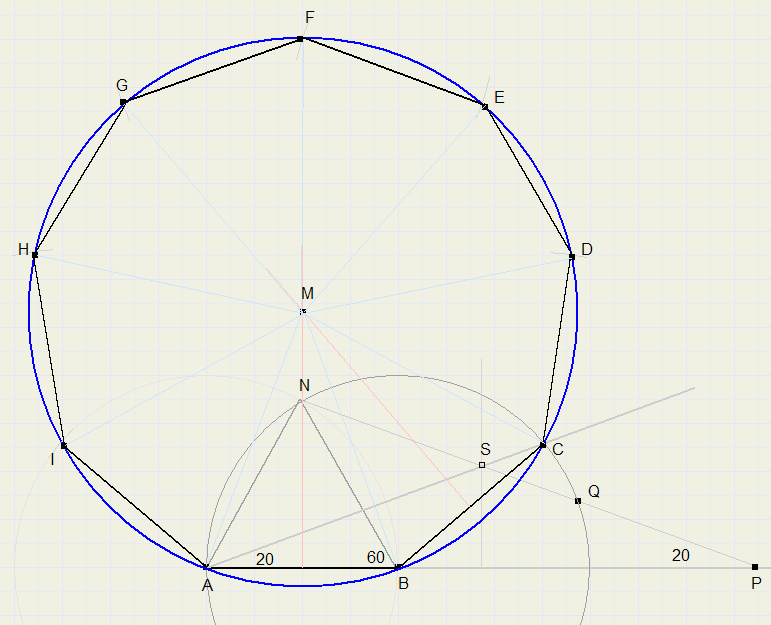
-
1. choose length of edge AB (say 4 cm.)
2. extend AB
3. construct equilateral triangle NAB
4. draw arc around B, radius BN.
5. place 2 markers on ruler with distance AB
6. place ruler along point N, intersecting AB extension in point P, intersection with circle is Q.
7. shift ruler until PQ = AB (markers are at P and Q)
8. LNPA = 20 degrees. We reflect P to A.
9. construct perpendicular bisector of AP, intersection with NP is S
10. draw line through points A and S, LSAB = 20 degrees
11. extend AS, C is intersection with circle having center B and radius AB.
12. construct perpendicular bisectors of AB and BC, their intersection is point M.
13. draw circle around M with radius MB.
14. adjust compasses to AB (= BC) and draw arcs around A, B and intersections D, E, F, G, H, I with circle.
15. ABCDEFGHI is the polygon we wanted.
-
a regular 9 edge polygon divides its circumsrcibed circle in arcs of 40 degrees.
1...8 constructs LCAB = 20 degrees (holds arc of 40 degrees)
point M is the intersection of 2 perpendicular bisectors of the edges.
Another way to construct a 400 angle
This construction was invented by mr. Fedde Reeskamp. (Thanks for his nice work)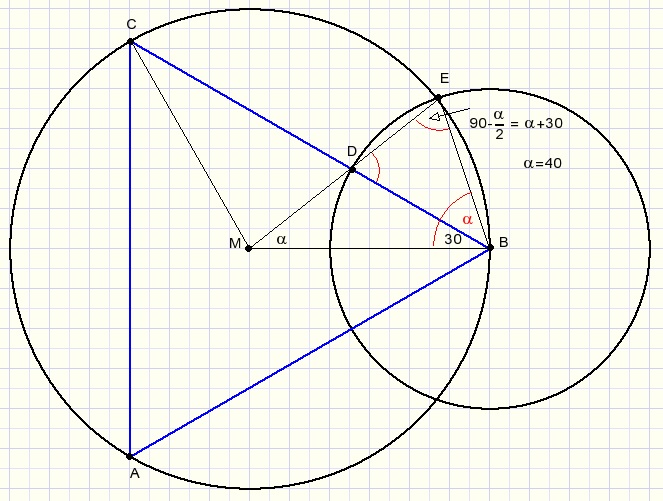
From point B of equilateral triangle ABC with circumscribed circle a new circle is drawn
such that points M,D,E are on a straight line.
BE is the side of a regular 9 angle polygon.
At first glance the ratio of the circle radius is 3:2.
However this is not true.
If this ratio is choosen the angle will be 38,93 degrees, not 40.

