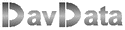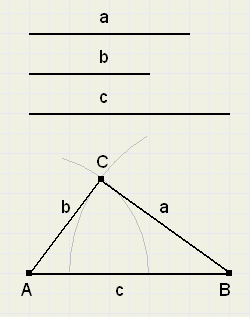
Triangles and Sides Problem Given are 3 lines with lengths a, b and c. Which conditions enable the construction of a triangle having a,b and c as sides? Refer to figure 1. below. The triangle has c as base. Angle C is the intersection of the circles with radii a and b, and centres A and B. fig.1 now look at figure 2. fig.2 In fig.1, the construction of a triangle was possible. In fig.2 it is not. The reason is clear : in fig. 2 , a en b together are smaller than c. De condition therefore can be written as the inequality : c < a + b Of course, also must be valid:: a < b + c .............and b < a + c The following is funny: If we call s half the perimeter of the triangle, then: a + b + c = 2s starting with the inequality a < b + c...............we may write (left and right : add a) 2a < a + b + c 2a < 2s.................so a < s This should be true for b and c as well, so we state: every side of a triangle must be smaller then half of the perimeter Another nice problem 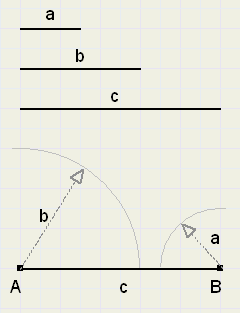Given is a equilateral triangle containing an arbitrary point P. From P, we add lines PA = a, PB = b and PC = c. Prove, that a, b and c always may be sides of a triangle. See figure 3 below: fig.3 Solution 1. ABC is equilateral, assume it's sides have length z. We observe: a < z ...................and also z < b + c ...........................combining: a < b + c and similar: b < a + c c < a + b Which concludes the proof. Solution 2. We rotate the triangle by 60 degrees, A being the centre of the rotation. So B arrives in C, C becomes C' en P becomes P'. see figure 4. 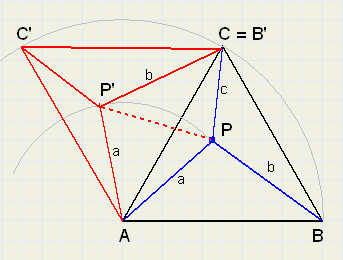fig.4 Triangle APP' is equilateral because LP'AP is 60 degrees and P'A = PA = a, so LPP'A = LP'PA = 60 degrees. So PP'= a and we notice that triangle CPP' has sides a,b and c. Quite surprising.