sudoku solver

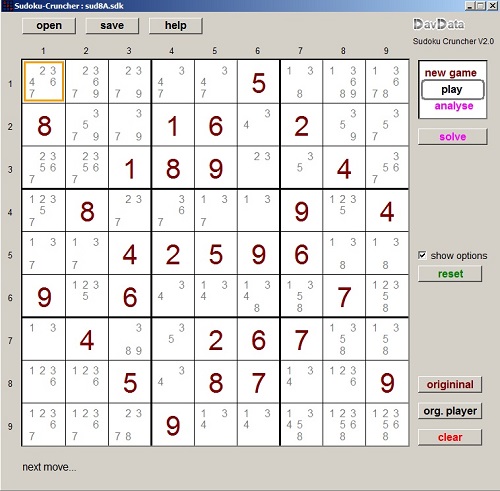
A sudoku solver program

reduced image of Sudoku program

A new version 2.0 of the sudoku solver is available.
This has more convenient buttons.

Download the Sudoku solver version 1.0

Download the Sudoku solver version 2.0

Contents

Sudoku-Cruncher Help

contents:

Options

The Sudoku-cruncher is a (Windows) program that provides

Controls

Menu buttons are placed at the top of the form:

- open	: press to open a game previously saved
- save	: press to save the present game
- help	: press to open this page

Game selection is by mouseclick on texts at the right top:

- new game	: manually enter a new game
- play	: enter digits to find a solution
- analyse	: generate hints

Entering a new game

Click on new game text.
An orange cursor points to the field where numbers may be placed.
Typing a number 1..9 enters this number in the cursor field.
Number color is brown, indicating an original game number, that cannot be modified later.
Delete a number by placing cursor on field and pressing the delete key.
The cursor is moved by the cursor keys, space key and backspace key.

If the options display (upper right) is checked, numbers may be entered by a mouseclick
on the option.

Press clear button to remove all numbers.

Playing a game

The player searches for solutions.
Typed numbers are placed in the cursorfield.
Number color is black, indicating user supplied numbers.
Delete a number by placing cursor in field, then press delete key.

Press original button to remove all black numbers.

If options display is checked the following options are valid:

Solver help

1. Brute force solutions
Press solve menu button below game selections.
Press solve button at lower right.
This button solves all games however difficult.
Numbers added are orange.
Press solve again to search for more solutions.
(A good sudoku puzzle has one unique solution).
If more solutions are found, the sudoku puzzle is wrong.

Press the org.user button to remove orange numbers and to restore game to
the state after the last user move.

2. Assistance.
Press analyse generate a hint.
Next, press the space bar to implement the hint, press again for next hint.
Press escape to leave analyse mode and return to play mode.

All analyses methods search for redundant options to be removed.
There are 3 investigations:
A.
Reduction within row, column or group, see picture

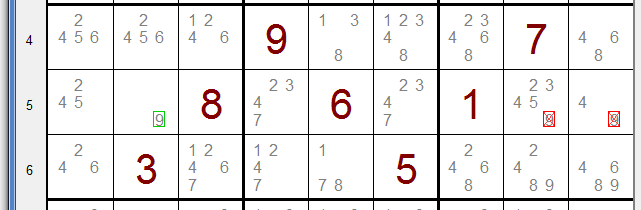
Row 5, column 2 has a single 9 option.
So, this field must have number 9 and the 9 options in other fields of row 5 may be removed.
These redundant options are marked by a red rectangle and X cross.

Please look at the following example:

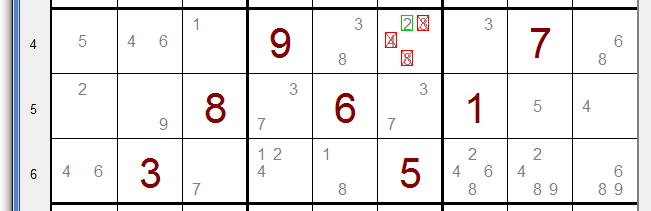
Row 4, column 6 is the only field in row 4 that has option 2.
The other options in this field are redundant and may be removed.

Of course, similar situations are applicable to columns and groups.
These are examples of a more general rule, see strategies for an explanation.

The above rules suffice to solve 2 (**) to 4 (****) star sudoku's.

B.
Reduction by interaction between groups and rows/columns.
Please see the picture below:

Pictured are 3 groups (3*3) fields each.
Each group is made of 3 horizontal triples (adjacent fields in row)
Look at row 5:
The "8" option is only present in columns 1 and 3.
So some field of triple 2 of this group gets an "8" number.
Therefore, the "8" options in triples 1 and 3 are redundant and red-crossed.
Of course, there are many variations (such as vertical triples) to this rule.
See strategies for a more complete explanation.

The above example was obtained from a 9 star sudoku.
Up to 5 star sudoku games, this situation seldom arises.

C.
If methods A. and B. fail to make a reduction of options,
for each field and option the number is filled in temporarily and method A. reductions are tried.
If the number was wrong, reduction may cause an empty field somewhere without options.
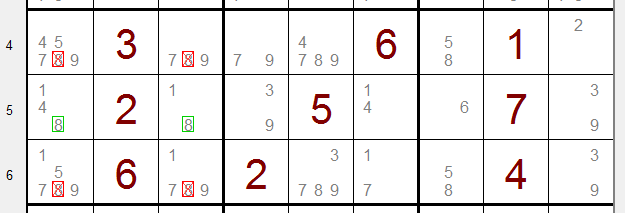
See picture below:

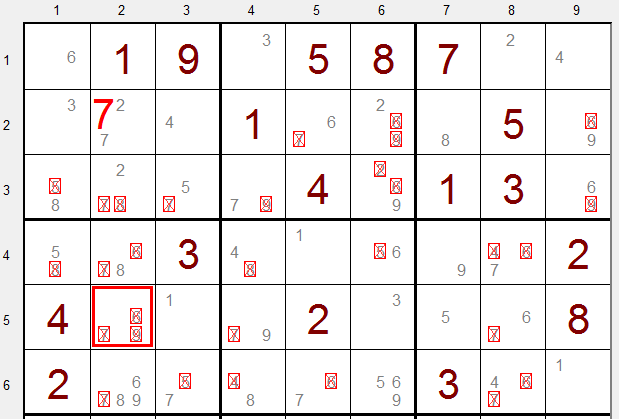
A "7" was entered temporarily in row 2, column 2.
As a result, the row 5 column 2 field lost all options.
So, the "7" option is never able to produce a solution and must be removed.

This methods allows for the solution of up to 12 star sudoku's.

To exit the analyse state at any time, press stop.

Saving a game

Press the save menu button and follow the dialog.
File names get the .sdk extension.

Open a game

Press the open menu button and follow the dialog.

Another method is to double click on a *.sdk file.
The first time, Windows will ask for the application.
Instruct Windows to use the sudoku-cruncher.exe.
From this moment, *.sdk files will be displayed with the sudoku-cruncher icon.

Game description

Sudoku is a number puzzel.
There are 9*9 fields, organized as 9 rows, 9 columns and 9 (3*3 field) groups.
A solved puzzel has the numbers 1..9 placed once in each rows, columns or groups.
Initial games have 17 (minimal) up to 30 numbers written already.
The player has to fill in the empty fields using logic reasoning and searching.

Sudoku puzzles come in great variety of difficulty.
The examples in daily newspapers are of level 2..4 (stars).
The described A. reduction method is sufficient to solve most of these puzzles.
However for the 4 star puzzles the search is harder and there are less opportunities for option reduction.
When options are displayed, it becomes much easier to solve a puzzle.

Strategies

Here follows a more general description of the A. and B. reduction methods.

A.
The most simple way to solve a puzzle is to start with an empty field and try all 9 numbers.
If only one number fits, it should be placed in this field.

Another way is to start with a number and try to place this number at the empty fields of a row, column or group.
If the number fits in only one field, this is the place.

The above methods are just simple examples of a more general rule.
Look at the next picture:

Options 7,9 only occur in columns 3,4.
So, they cannot show up in other columns.

This is the general rule:
If we select K fields (of 9) and these fields have together K options,
these options cannot show up in other fields then K.
So we may drop all these options in fields outside K.

For K = 1: one option in a field drops this option in the 8 other fields.
For K = 8: 8 fields have 8 options. So all these options may be dropped in field 9 (not K).
This is the "number fits in one field only" case.

In the program, combinations are counted for K=1 to K=4.
The K fields and (9-K) not K fields are considered as selections.

Simple puzzles mostly need K=1 solutions.
4 star puzzles use a lot of K=8 solutions.

B.
This is the interaction between groups and rows/columns.

Here the game is regarded as triples: 3 fields horizontally or vertically.
A group is made of 3 horizontal triples, or 3 vertical triples.
A row has 3 horizontal triples, a column has 3 vertical triples.

Now look at the picture below:

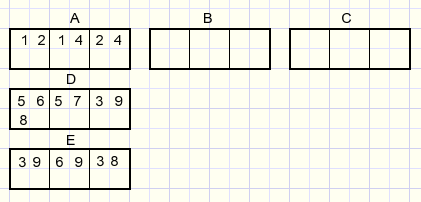
Triples ADE make a group. Triples ABC make a row.
Options 1,2,4 only occur in triple 1 not in triples 2,3.
So these numbers cannot show up in triples 2,3 of the row.

Let's call triples B,C complementary to triples D,E.
Starting with a triple (A), there are 2 other complementary triples (BC, DE).

This is the general rule:
If two triples of a group, column or row do not have options P,
these P options also are absent in the complementary triples.

Again: options that are absent in triples DE are also absent in BC.
Absent options in BC are also absent in DE.

Installation

Sudoku-cruncher is freeware.
It runs under all Windows versions.
There is no installation procedure: just copy the sudoku-cruncher.exe file to a folder of choice.

The programming language is Delphi (7).

Delphi source code

Interested in the source code of this Delphi-7 project?
click [HERE]

Several puzzles are included, including the most difficult one in the world.

A key procedure in this Sudolu solver is the combinations counter.
This procedure sequentially selects 1..4 fields from 9 for examination.
Look [ HERE ] for a description and source code.