Eindexamen meetkunde MULO 1920

Hieronder tref je aan het eindexamen meetkunde van de M.U.L.O. - B in 1920.
De uitwerking is van mijzelf.
Waar nodig voeg ik wat theorie toe.

Tijdsduur : 1,5 uur voor 3 vraagstukken.

1.
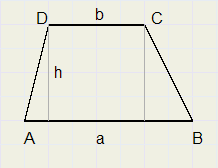
Gegeven is een trapezium.
Construeer (met passer en liniaal) een vierkant, waarvan de oppervlakte gelijk is aan 3/5 de deel
van de oppervlakte van het trapezium.

Opmerking: de oppervlakte van (bijvoorbeeld) vierhoek ABCD noteer ik als [ABCD].

Uitwerking:
Bekijk het trapezium in figuur 1. hieronder:

AB = a, CD = b, hoogte = h
    [ABCD] =
    (a + b) h
    2

Laat vierkant PQRS het gevraagde vierkant zijn.
Dat moet gelden:
    [PQRS] =
    3 (a + b) h
    10

    PQ =
    \
    3 (a + b) h
    10
Voor het gemak stellen we een nieuwe lengtemaat vast, de dav, h = 1 (dav), zodat bovenstaande formule overgaat in
    PQ =
    \0.3 (a + b)
Dat ziet er een stuk vriendelijker uit.

De lengte a+b is eenvoudig met een passer op een rechte lijn af te ztten.
Deze lengte verdrievoudigen we ook weer door die afstand met de passer af te zetten.
Deze afstand moet vervolgens door 10 worden gedeeld.
Zie figuur 2 hieronder:


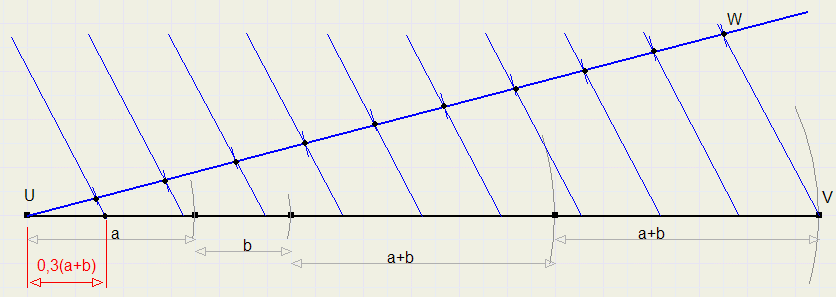
    UV = 3(a+b)
Trek nu een lijn door U enigszins omhoog.(blauw getekend).
Pas op deze lijn 10 gelijke stukjes af. Noem het laatste punt W.
Trek de lijn VW en alle blauwe lijnen evenwijdig hieraan.
De afstand 3(a+b) is in de figuur in rood aangegeven.

Opmerking:
We gebruiken hier de stelling:
"Twee snijdende lijnen verdelen evenwijdige lijnen in stukken met dezelfde verhouding".
Zo worden lijnstukken UW en UV beide in 10 gelijke stukken verdeeld.

Resteert de vraag hoe we de wortel construeren uit een gegeven lengte.

De Wortelconstructie
bekijk figuur 3



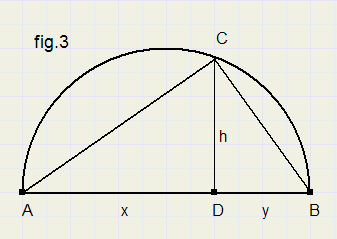
De hoogtelijn uit C verdeelt de middellijn AB in stukken van x en y lang.
LC = 90 graden (stelling van Thales)

AC2 = x2 + h2
BC2 = y2 + h2
en omdat
AC2 + BC2 = AB2:

x2 + h2 + y2 + h2 = (x +y)2

x2 + 2h2 + y2 = x2 + 2xy + y2

h2 = xy

h = 
\x y

Door y = 1 te nemen kan zo de wortel uit x worden geconstrueerd.

Op een lijn zetten we nu de waarde 0,3(a+b) af met daarvoor de lengte 1 (was hoogte van het trapezium).
Zie figuur 4


Deze lengte 1 + 0,3(a+b) is de middellijn van een cirkel.
We construeren die cirkel en ook de hoogtelijn h.
h = PQ.
Het groene vierkant met zijden h in figuur 4 is het gevraagde vierkant PQRS.

2.
In een cirkel met straal R beschrijft men een DABC zodanig, dat AB de zijde van de ingeschreven regelmatige
driehoek en AC de zijde van de ingeschreven regelmatige vierhoek is.
De hoogtelijn AH wordt getrokken.
Te bewijzen:
a. HC = AC / 2
b. HA = HB

Uitwerking:
Zie figuur 5. hieronder:


a.
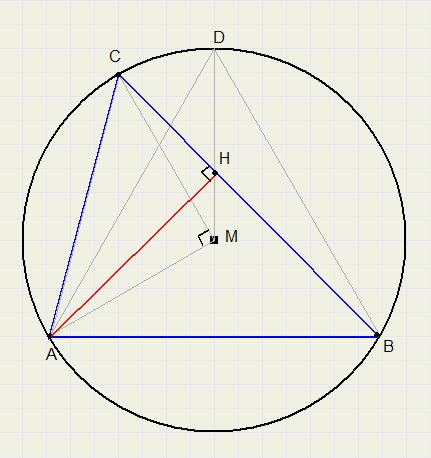
LACB = 1/2 boog AB = 60°
DAHC is dus de helft van een gelijkzijdige driehoek, zodat
HC = AC / 2

b.
LABC = 1/2 boog AC = 45°
DABH is gelijkbenig, zodat
AH = HB

Stelling: In een driehoek liggen tegenover gelijke hoeken gelijke zijden en omgekeerd.

Opmerking:
Een "koorde" is een lijnstuk waarvan begin en eindpunt op dezelfde cirkel liggen.
Een hoek die gevormd wordt door twee koorden die elkaar op de cirkel snijden heet "omtrekshoek".
Onder de "booglengte" van een cirkelboog verstaan we de hoek van de lijnen die begin en eindpunt
met het middelpunt van de cirkel verbinden.
Stelling:
"Een omtrekshoek is gelijk aan de helft van de cirkelboog waarop hij staat".

zie figuur 6.


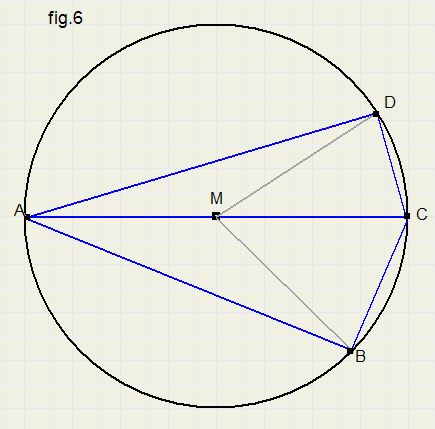
Uit de definitie volgt: boog CD = LCMD.
Er geldt:
LCMD = LDAM + LADM............
..............{een buitenhoek van een driehoek is gelijk aan de som van de niet aanliggende binnenhoeken}
en omdat DAMD gelijkbenig is:
LDAC = LDMC / 2 = 1/2 boog CD
ook:
LCAB = 1/2 boog BC...........dus..........
LDAB = 1/2 boog BD


3.
Van een gelijkbenig trapezium zijn de evenwijdige zijden 42 en 12 cm. en de opstaande zijden 39cm.
Bereken de straal van de omgeschreven cirkel van dat trapezium.

Bij deze opgave voelde ik mij aanvankelijk wat ongemakkelijk.
Het is namelijk veel rekenwerk, terwijl in 1920 geen rekenmachines werden gebruikt tijdens de examens.
Misschien hadden de leerlingen tabellenboekjes met kwadraten en wortels.
Gezien de 1,5 uur voor dit examen kan het niet de bedoeling zijn geweest dat er veel tijd in rekenwerk werd gestoken.
Ik zocht dus in oude meetkunde boekjes naar handige stellingen,
waarvan de leerlingen er vele uit het hoofd moesten kennen.
Het gebruik van stellingen spaart veel werk uit.
Immers, dat rekenwerk is al verricht bij het bewijzen van de stelling.

Voor de oplossing van dit vraagstuk maak ik gebruik van de formule:
    R =
    a b c
    4 O
In woorden: de straal van de omgeschreven cirkel van een driehoek met zijden a,b en c
is gelijk aan het product van de zijden gedeeld door 4 maal de oppervlakte van de driehoek.
Ik zal deze formule later bewijzen.

Ook gebruik ik de stelling van Ptolemaeus:
"Van een koordenvierhoek is het product van de diagonalen gelijk aan de som van de producten
van de overstaande zijden."

Deze stelling zal ik ook later bewijzen.

bekijk nu figuur 7 hieronder:


Stelling van Ptolemeus:
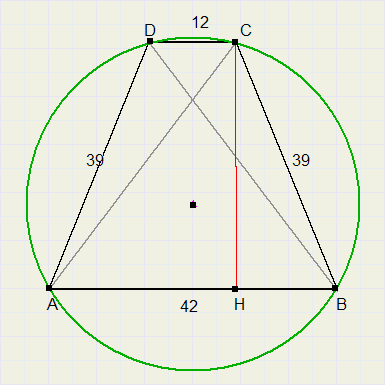
    AC2 = 12 * 42 + 39 * 39 = 2025
    AC = 45.

    Formule voor de straal van de omgeschreven cirkel van DABC:

    R = 
    42 · 39 · 45
    4 O
Nu oppervlakte O berekenen van DABC.
Trek hoogtelijn CH en pas de stelling van Pythagoras toe: ........{HB = (42 - 12) / 2 = 15}
    HC2 = 392 - 152 = 1296
    HC = 36

    O = 42 * 36 / 2 = 756..............zodat............

    R = 
    42 · 39 · 45
    4 · 756
     = 24 , 375

Bewijs van de gebruikte formule en stelling.

Straal R van de omgeschreven cirkel van een driehoek met zijden a,b en c........: R = 
a b c
4 O

Zie figuur 8 hieronder:


LACB = boogAB / 2 = boog BE.
LEMB = boog BE...............dus...........
LACB = LMB

We passen nu de stelling toe:
"als twee driehoeken een gelijke hoek hebben, dan verhouden hun oppervlakten zich
als het product van hun zijden om die hoek".
Het bewijs laat ik aan de lezer over.

[ABC] : [DMB] = (AC * BC) : (DM * BM)

(H * c/2) : (h * c/4) = (a * b) : (h * R)..................vermenigvuldigen met h.........

(H * c/2) :(c/4) = (a * b) : R...................bedenk, dat O = [ABC] = H* c/2...................

O : (c/4) = (a * b) : R.......dus .........R = ........enzovoorts

Bewijs van de stelling van Ptolemaeus.
"Van een koordenvierhoek is het produkt van de diagonalen gelijk aan de som van de producten van
de overstaande zijden".

Zie figuur 9 hieronder:


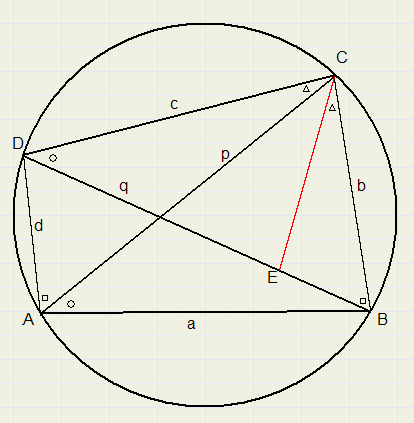
We zien koordenvierhoek ABCD, met AC = p en BD = q
Gelijke hoeken hebben eenzelfde merktekentje.
DCEB is zodanig getekend, dat LECB = LDCA

Wegens gelijke hoeken geldt...............DACD ~ DBCE.............{let op juiste volgorde van letters}
zodat
p : d = b : BE...........BE = bd / p

Ook is DACB ~ DDCE
zodat
p : a = c : DE..........DE = ac/p

q = BE + DE = (ac + bd)/p.................zodat

pq = ac + bd