p berekenen

Inleiding
Bij berekeningen aan cirkels en bollen treffen we het getal p aan.
Uitgaande van een straal R is:
    omtrek cirkel2pR
    oppervlakte cirkelpR2
    oppervlakte bol4pR2
    inhoud bol(4/3)pR3
p is ongeveer 3,141592654.....maar er bestaat geen getal, dat precies gelijk is aan p.
Daarom wordt in formules ook liever p gebruikt dan 3,14...Je kunt dan net zoveel decimalen
invullen als nodig is voor de gewenste nauwkeurigheid.
p is alleen te benaderen: hoe meer rekenwerk we er voor over hebben,
hoe nauwkeuriger het resultaat.

Dit artikel gaat over een van de vele methoden om p te vinden,
namelijk door een cirkelboog te benaderen met een regelmatige veelhoek.

De Griekse wis- en natuurkundige Archimedes heeft omstreeks 250 v. Chr. deze methode al gebruikt.
Hij vond toen met een regelmatige 96 hoek, dat p moest liggen tussen
22
7
 en
223
71
In 1585 gaf Metius een benadering voor p met 6 decimalen,
Vieta had echter in 1579 met behulp van een regelmatige 393216 hoek p al op 9 decimalen
nauwkeurig berekend.
Adriaen van Roomen bepaalde in 1579 p op 16 decimalen,
Ludolf van Ceulen zette dit werk voort en bepaalde in 1621 p met een nauwkeurigheid van 35 decimalen,
gebruik makend van een regelmatige 265 hoek.
Tegenwoordig zijn, dankzij computers en reeksontwikkelingen, miljoenen decimalen van p bekend.
Praktische betekenis heeft dit niet meer.

Lambert bewees in 1761 dat p een onmeetbaar getal is.
Lindemann toonde in 1882 aan, dat p ook een transcendent getal is,
d.w.z. dat p geen wortel kan zijn van een (hogere macht) vergelijking.
Hiermee was eindelijk bewezen, dat er geen methode bestaat om met passer en liniaal een lijnstuk te
construeren dat gelijke lengte heeft als de omtrek van een gegeven cirkel.

De methode
    fig.1fig.2fig.3
In fig.1 wordt de omtrek van de cirkel benaderd door de omtrek van een vierkant,
in fig.2 door een 8 hoek en in fig.3 door een 16 hoek.
Uitgaande van een cirkel met straal 1, zal de halve omtrek gelijk zijn aan p.
Hoe meer hoeken, hoe beter de benadering.
Maar voor het echte werk begint, een aanloopje.

De Koorden Halverings Formule
Een koorde is een lijnstuk, waarvan begin- en eindpunt op een cirkel liggen.
    fig.4
In fig.4 zijn AB en AC koorden. MA is dat niet.
We zullen nu, uitgaande van de lengte van AB, de lengte van koorde AC berekenen.
Daarbij nemen we MA = MB = MC = 1.
De halve cirkelboog heeft dan precies de lengte p.

Wegens de symmetrie staat AB loodrecht op MC, zodat de stelling van Pythagoras kan
worden toegepast.



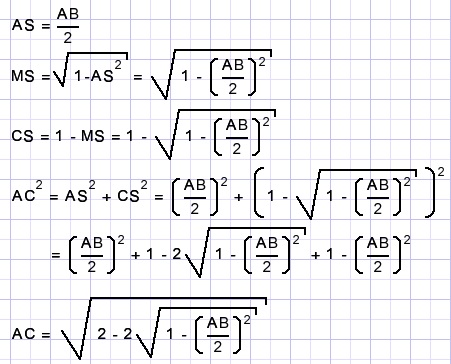
Dit is de koorden halverings formule.

p benaderen
bekijk fig.5 hieronder:
    fig.5
We stellen:
    AB = x0
    AC = x1
    AD = x2
 AB, de middellijn, is ook een koorde en wel met lengte 2.
Dat is een zeer slechte benadering van p.
Een iets minder slechte benadering is 2.AC en alweer iets beter: 4.AD.

Veel beter:
    p » 2n.xn voor hoge waarden van n.
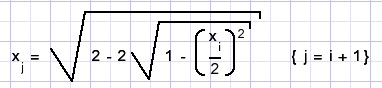
Met x0,1,2... wordt de koorden halverings formule:



uitgaande van AB = x0 = 2, kan x1 worden berekend,
met x1 weer x2, met x2 weer x3 enzovoorts....
Dit is een iteratief proces.

Bovengrens
De aldus berekende waarde van p zal iets te klein zijn,
omdat -in-geschreven veelhoeken worden gebruikt.
Door ook de -om-geschreven veelhoeken te berekenen ontstaat een bovengrens voor p.
Zie fig.6 hieronder:
    fig.6
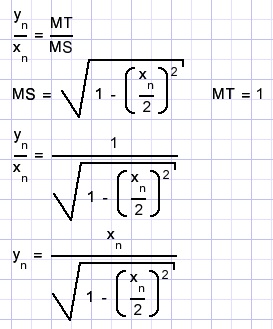
Uit de gelijkvormigheid van de in- en omgeschreven driehoeken volgt:



Aktie!
Klik op de knopjes in de figuur hieronder om stap voor stap p beter te benaderen.
De cirkel heeft een straal van 1.